Matlab微分和導數

MATLAB提供用於計算符號導數的diff命令。 以最簡單的形式，將要微分的功能傳遞給diff命令作為引數。

例如，計算函式的導數的方程式 -

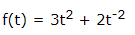
例子

建立指令碼檔案並在其中鍵入以下程式碼 -

syms t
f = 3*t^2 + 2*t^(-2);
diff(f)

執行上面範例程式碼，得到以下結果 -

Trial>> syms t
f = 3*t^2 + 2*t^(-2);
diff(f)

ans =

6*t - 4/t^3

以下是使用Octave 計算的寫法 -

pkg load symbolic
symbols

t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)

執行上面範例程式碼，得到以下結果 -

ans =

6*t - 4/t^3

基本微分規則的驗證

下面簡要說明微分規則的各種方程或規則，並驗證這些規則。 為此，我們將寫一個第一階導數f'(x)和二階導數f「(x)。

以下是微分的規則 -

規則 - 1

對於任何函式f和g，任何實數a和b是函式的導數：

h(x) = af(x) + bg(x)相對於x，由h’(x) = af’(x) + bg’(x)給出。

規則 - 2

sum和subtraction規則表述為：如果f和g是兩個函式，則f'和g'分別是它們的導數，如下 -

(f + g)' = f' + g'

(f - g)' = f' - g'

規則 - 3

product規則表述為：如果f和g是兩個函式，則f'和g'分別是它們的導數，如下 -

(f.g)' = f'.g + g'.f

規則 - 4

quotient規則表明，如果f和g是兩個函式，則f'和g'分別是它們的導數，那麼 -

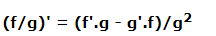
規則 - 5

多項式或基本次冪規則表述為：如果y = f(x)= x^n，則 -

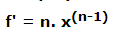
這個規則的直接結果是任何常數的導數為零，即如果y = k，那麼為任何常數 -

f' = 0

規則 - 5

chain規則表述為 - 相對於x的函式h(x)= f(g(x))的函式的導數是 -

h'(x)= f'(g(x)).g'(x)

例子
建立指令碼檔案並在其中鍵入以下程式碼 -

syms x
syms t
f = (x + 2)*(x^2 + 3)
der1 = diff(f)
f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)
f = (x^2 + 1)^17
der5 = diff(f)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)

執行上面範例程式碼，得到 以下結果 -

f =
 (x^2 + 3)*(x + 2)

 der1 =
 2*x*(x + 2) + x^2 + 3

f =
 (t^(1/2) + t^3)*(t^2 + 3)

 der2 =
 (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)

f =
 (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)

der3 =
 (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)

 f =
 (2*x^2 + 3*x)/(x^3 + 1)

der4 =
 (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2

f =
 (x^2 + 1)^17

der5 =
 34*x*(x^2 + 1)^16

f =
1/(t^3 + 3*t^2 + 5*t - 9)^6

der6 =
 -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7

以下是對上面範例的Octave寫法 -

pkg load symbolic
symbols
x=sym("x");
t=sym("t");
f = (x + 2)*(x^2 + 3) 
der1 = differentiate(f,x) 
f = (t^2 + 3)*(t^(1/2) + t^3) 
der2 = differentiate(f,t) 
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) 
der3 = differentiate(f,x) 
f = (2*x^2 + 3*x)/(x^3 + 1) 
der4 = differentiate(f,x) 
f = (x^2 + 1)^17 
der5 = differentiate(f,x) 
f = (t^3 + 3* t^2 + 5*t -9)^(-6) 
der6 = differentiate(f,t)

指數，對數和三角函式的導數

下表提供了常用指數，對數和三角函式的導數，

例子
建立指令碼檔案並在其中鍵入以下程式碼 -

syms x
y = exp(x)
diff(y)
y = x^9
diff(y)
y = sin(x)
diff(y)
y = tan(x)
diff(y)
y = cos(x)
diff(y)
y = log(x)
diff(y)
y = log10(x)
diff(y)
y = sin(x)^2
diff(y)
y = cos(3*x^2 + 2*x + 1)
diff(y)
y = exp(x)/sin(x)
diff(y)

執行上面範例程式碼，得到以下結果 -

y =
 exp(x)
 ans =
 exp(x)


y =
x^9
 ans =
 9*x^8

y =
 sin(x)
 ans =
 cos(x)

y =
 tan(x)
ans =
 tan(x)^2 + 1

 y =
 cos(x)
 ans =
 -sin(x)

y =
 log(x)
 ans =
 1/x

y =
 log(x)/log(10)
 ans =
 1/(x*log(10))

y =
 sin(x)^2
  ans =
 2*cos(x)*sin(x)

 y =

cos(3*x^2 + 2*x + 1)
 ans =
 -sin(3*x^2 + 2*x + 1)*(6*x + 2)

y =
 exp(x)/sin(x)
 ans =
 exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2

以下程式碼是上面程式碼的Octave寫法 -

pkg load symbolic
symbols

x = sym("x");
y = Exp(x)
differentiate(y,x)

y = x^9
differentiate(y,x)

y = Sin(x)
differentiate(y,x)

y = Tan(x)
differentiate(y,x)

y = Cos(x)
differentiate(y,x)

y = Log(x)
differentiate(y,x)

% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)

y = Sin(x)^2
differentiate(y,x)

y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)

y = Exp(x)/Sin(x)
differentiate(y,x)

計算高階導數

要計算函式f的較高導數，可使用diff(f，n)。

計算函式的二階導數公式為 -

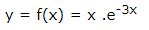
f = x*exp(-3*x);
diff(f, 2)

MATLAB執行上面程式碼將返回以下結果 -

ans =
9*x*exp(-3*x) - 6*exp(-3*x)

以下是使用Octave重寫上面範例，程式碼如下 -

pkg load symbolic
symbols

x = sym("x");
f = x*Exp(-3*x);

differentiate(f, x, 2)

例子
在這個例子中，要解決一個問題。由給定函式y = f(x)= 3sin(x)+ 7cos(5x)，來找出方程f「+ f = -5cos(2x)是否成立。

建立指令碼檔案並在其中鍵入以下程式碼 -

syms x
y = 3*sin(x)+7*cos(5*x);  % defining the function
lhs = diff(y,2)+y;        %evaluting the lhs of the equation
rhs = -5*cos(2*x);        %rhs of the equation
if(isequal(lhs,rhs))
    disp('Yes, the equation holds true');
else
    disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

執行檔案時，會顯示以下結果 -

No, the equation does not hold true
Value of LHS is: 
-168*cos(5*x)

以上是上面範例的Octave寫法 -

pkg load symbolic
symbols

x = sym("x");
y = 3*Sin(x)+7*Cos(5*x);           % defining the function
lhs = differentiate(y, x, 2) + y;  %evaluting the lhs of the equation
rhs = -5*Cos(2*x);                 %rhs of the equation

if(lhs == rhs)
    disp('Yes, the equation holds true');
else
    disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

查詢曲線的最大和最小值

如果正在搜尋圖形的區域性最大值和最小值，基本上是在特定地點的函式圖上或符號變數的特定值範圍內查詢最高點或最低點。

對於函式y = f(x)，圖形具有零斜率的圖上的點稱為固定點。 換句話說，固定點是f'(x)= 0。

要找到微分的函式的固定點，需要將導數設定為零並求解方程。

範例

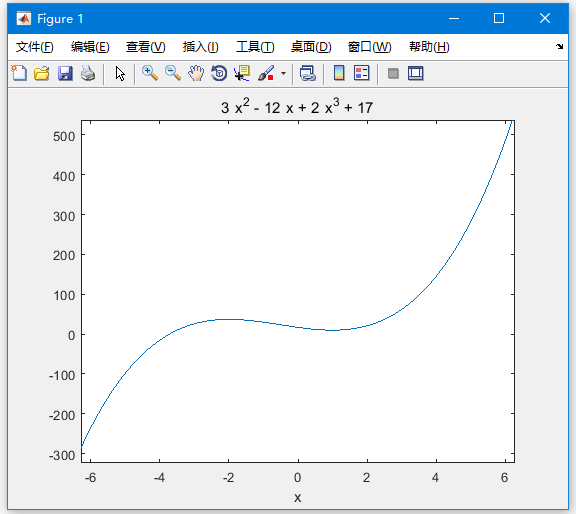
要找到函式f(x)= 2x3 + 3x2 - 12x + 17的固定點

可參考以下步驟 -

首先輸入函式並繪製圖，程式碼如下 -

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;  % defining the function
ezplot(y)

執行上面範例程式碼，得到以下結果 -

以上是上面範例的Octave寫法 -

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y)
print -deps graph.eps

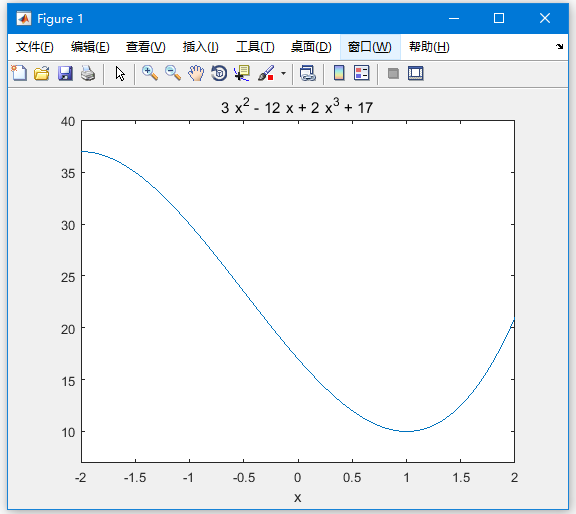
我們的目標是在圖上找到一些區域性最大值和最小值，假設要找到圖中間隔在[-2,2]的區域性最大值和最小值。參考以下範例程式碼 -

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;  % defining the function
ezplot(y, [-2, 2])

執行上面範例程式碼，得到以下結果 -

以下是上面範例的Octave寫法 -

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y, [-2, 2])
print -deps graph.eps

接下來，需要計算導數。

g = diff(y)

MATLAB執行程式碼並返回以下結果 -

g =

6*x^2 + 6*x - 12

以下是上面範例的Octave寫法 -

pkg load symbolic
symbols

x = sym("x");

y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

接下來求解導數函式g，得到它變為零的值。

s = solve(g)

MATLAB執行程式碼並返回以下結果 -

s = 
     1
    -2

以下是上面範例的Octave寫法 -

pkg load symbolic
symbols

x = sym("x");

y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])

這與我們設想情節一致。 因此，要評估臨界點x = 1，-2處的函式f。可以使用subs命令替換符號函式中的值。

subs(y, 1), subs(y, -2)

MATLAB執行程式碼並返回以下結果 -

ans =
 10
ans =
 37

以下是上面範例的Octave寫法 -

pkg load symbolic
symbols

x = sym("x");

y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

roots([6, 6, -12])

subs(y, x, 1), subs(y, x, -2)

因此，在間隔[-2,2]中函式f(x)= 2x^3 + 3x^2 - 12x + 17的最小值和最大值分別為10和37。

求解微分方程

MATLAB提供了用於求解微分方程的dsolve命令。

找到單個方程的解的最基本的dsolve命令形式是 -

dsolve('eqn')

其中eqn是用於輸入方程式的文字串。

它返回一個符號解，其中包含一組任意常數，MATLAB標記C1，C2等等。
還可以為問題指定初始和邊界條件，以逗號分隔的列表遵循以下公式：

dsolve('eqn','cond1', 'cond2',…)

為了使用dsolve命令，導數用D表示。例如，像f'(t)= -2 * f + cost(t)這樣的等式輸入為 -

'Df = -2*f + cos(t)'

較高階導數由D導數的順序表示。

例如，方程f"(x) + 2f'(x) = 5sin3x應輸入為 -

'D2y + 2Dy = 5*sin(3*x)'

下面來看一個一階微分方程的簡單例子：y'= 5y。

s = dsolve('Dy = 5*y')

MATLAB執行程式碼並返回以下結果 -

s =
 C2*exp(5*t)

再來一個二階微分方程的例子：y「-y = 0，y(0)= -1，y'(0)= 2。

dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')

MATLAB執行程式碼並返回以下結果 -

ans =
 exp(t)/2 - (3*exp(-t))/2