本篇繼續參照高翔老師《視覺SLAM十四講從理論到實踐》，講解四元數表示變換。博文將原第三講分為四部分來講解：1、旋轉矩陣和變換矩陣；2、旋轉向量與羅德里格斯公式；3、尤拉角與萬向（節）鎖；4-1、四元數表示變換；4-2、四元數差值。本文相對於原文會適當精簡，同時為便於理解，會加入一些註解和補充知識點，本篇為第四部分：四元數表示變換，另外三部分請參照博主的其他博文。
本篇文章，博主猶豫了很久，一是四元數東西較多，怕寫不好；二是已經有些人寫的非常好，基本疑問都解決了，後來者難以超越，博主在附錄會做推薦；三是作取捨真的太難，寫的太多篇幅太長，寫的少又怕涵蓋不全。然而自己挖的坑哭著也要填上，博主會盡量釋疑，做一些修補工作，也只求沒有錯誤紕漏。另外寫的不好的地方還請見諒，也歡迎多提意見，博主會盡量完善。

1. 四元數的定義

1.1 為什麼使用四元數

旋轉矩陣用9個量描述3自由度的旋轉，具有冗餘性；尤拉角和旋轉向量是緊湊的，但具有奇異性。事實上，我們找不到不帶奇異性的三維向量描述方式。
回憶之前學習過的複數，我們用複數集$\mathbb{C}$表示複平面上的向量，可以表示為$z=a+bi$的形式，其中$a,b\in R$而且$i^2=-1$，而複數的乘法則表示複平面上的旋轉：例如，乘上覆數$i$相當於逆時針把一個復向量旋轉$90^{\circ }$。類似的，在表達三維空間旋轉時，也有一種類似於複數的代數：四元數（Quaternion）。四元數是Hamilton找到的一種擴充套件的複數。它既是緊湊的，也沒有奇異性。如果說缺點，四元數不夠直觀，其運算稍複雜些。

1.2 複數與四元數

把四元數與複數類比可以幫助你更快地理解四元數。例如，當我們想要將複平面的向量旋轉$\theta$角時，可以給這個復向量乘以$e^{i\theta }$，這是極座標表示的複數，它也可以寫成普通的形式，只要用尤拉公式即可：$$e^{i\theta }=cos\theta +sin\theta .$$
尤拉公式將指數函數的定義域擴大到了複數域，建立和三角函數和指數函數的關係，被譽為「數學中的天橋」。尤拉公式的簡單推導如下，$e^x$的泰勒展開式為：
$$e^x=1+x+\frac{1}{2!}{x}^2+\frac{1}{3!}{x}^3+\cdot \cdot \cdot$$將$x$替換為$i\theta$：
$$\begin{array}{rl}{e}^{i\theta }& =1+i\theta +\frac{1}{2!}(i\theta {)}^2+\frac{1}{3!}(i\theta {)}^3+\frac{1}{4!}(i\theta {)}^4+\frac{1}{5!}(i\theta {)}^5+\frac{1}{6!}(i\theta {)}^6+\frac{1}{7!}(i\theta {)}^7+\frac{1}{8!}(i\theta {)}^8+\cdot \cdot \cdot \\ & =1+i\theta -\frac{1}{2!}{\theta }^2-\frac{1}{3!}i{\theta }^3+\frac{1}{4!}{\theta }^4+\frac{1}{5!}i{\theta }^5-\frac{1}{6!}{\theta }^6-\frac{1}{7!}i{\theta }^7+\frac{1}{8!}{\theta }^8+\cdot \cdot \cdot \\ & =(1-\frac{{\theta }^2}{2!}+\frac{{\theta }^4}{4!}-\frac{{\theta }^6}{6!}+\frac{{\theta }^8}{8!}-\cdot \cdot \cdot )+i(\theta -\frac{{\theta }^3}{3!}+\frac{{\theta }^5}{5!}-\frac{{\theta }^7}{7!}+\cdot \cdot \cdot )\\ & =cos\theta +sin\theta .\end{array}$$當$\theta =\pi$時，帶入尤拉公式得到：$$e^{i\pi }=cos\pi +isin\pi =-1\Rightarrow e^{i\pi }+1=0$$其中$e^{i\pi }+1=0$就是尤拉恆等式，它被譽為上帝公式，因為$e、\pi 、i$、乘法單位元1、加法單位元0，這五個重要的數學元素全部被包含在內，在數學愛好者眼裡，彷彿一行詩道盡了數學的美好。尤拉公式的詳細說明可參見《尤拉公式之美》。
尤拉公式的右側正是一個單位長度的複數，所以在二維情況下，旋轉可以有單位複數來描述。類似的，可以看到，三維旋轉可以有單位四元數來描述。

1.3 四元數的形式

四元數的定義和複數非常類似，唯一的區別就是四元數有三個虛部，而複數只有一個。所有的四元數$q\in \mathbb{H}$（$\mathbb{H}$代表四元數的發現者William Rowan Hamilton）都可以寫成如下形式：$$\mathbf{q}=q_0+q_{1}i+q_{2}j+q_{3}k.$$其中$i,j,k$為四元數的三個虛部，這三個虛部滿足以下關係式：$$\{\begin{array}{c}{i}^2=j^2=k^2=-1\\ ij=k,ji=-k\\ jk=i,kj=-i\\ ki=j,ik=-j\end{array}.$$
如果把$i,j,k$看成三個座標軸，那麼它們與自己的乘法和複數一樣，相互之間的乘法和外積一樣。有時，人們也用一個標量和一個向量來表達四元數：$$\mathbf{q}=[s,v{]}^T,s=q_0\in \mathbb{R},v=[q_1,q_2,q_3{]}^T\in {\mathbb{R}}^3.$$這裡，$s$稱為四元數的實部，而$v$稱為它的虛部。如果一個四元數的虛部為0，則稱為實四元數。反之，若實部為0，則稱為虛四元數或純四元數。
如果$\Vert q\Vert =1$，那麼$q$是單位四元數。可以用單位四元數表示三維空間中任意一個旋轉，不過這種表達方式和複數有著微妙的不同。在複數中，乘以$i$意味著旋轉$90^{\circ }$，而在四元數中，乘以$i$對應著旋轉$180^{\circ }$，這樣才能保證$$ij=k$的性質。而$i^2=-1$，意味著繞$i$軸旋轉$360^{\circ }$後得到一個相反的東西，也就是要旋轉兩週才會和它原先的樣子相等。
下面我們看一下四元數之間的運演演算法則。

2. 四元數的運算

四元數和複數一樣，可以進行一系列的運算。常見的有四則運算、共軛、求逆、數乘等，下面分別介紹。
現有兩個四元數$q_a，q_b$，它們的向量表示為$[s_a,v_a{]}^T$，$[s_b,v_b{]}^T$，其中$v_a=x_{a}i+y_{a}j+z_{a}k，v_b=x_{b}i+y_{b}j+z_{b}k$，或者原始四元數表示為：$$q_a=s_a+x_{a}i+y_{a}j+z_{a}k，q_b=s_b+x_{b}i+y_{b}j+z_{b}k.$$那麼，其運算可表示如下：

1. 加法和減法$$q_a\pm q_b=[s_a\pm s_b,v_a\pm v_b]$$

2. 乘法
   乘法是把$q_a$的每一項與$q_b$的每一項相乘，最後相加，整理得：$$\begin{array}{rl}{q}_a{q}_b& =s_a{s}_b-x_a{x}_b-y_a{y}_b-z_a{z}_b\\ & +(s_a{x}_b+x_a{s}_b+y_a{z}_b-z_a{y}_b)i\\ & +(s_a{y}_b-x_a{z}_b+y_a{s}_b+z_a{x}_b)j\\ & +(s_a{z}_b+x_a{y}_b-y_a{x}_b-z_a{s}_b)k.\end{array}$$雖然稍微複雜，但形式上還是整齊有序的。如果寫成向量形式並利用內外積運算，該表達會更加簡潔：$$q_a{q}_b=[s_a{s}_b-v_a^T{v}_b,s_a{v}_b+s_b{v}_a+v_a\times v_b]$$這個結果也稱為$GraBmann$積，它是四元數與旋轉聯絡起來的關鍵。
   另外，由於最後一項外積的存在，四元數乘法通常是不可交換的，除非$v_a$和$v_b$在$\mathbb{R}$中共線，此時外項積為零。

3. 模長
   四元數的模長定義為：$$\Vert q_a\Vert =\sqrt{s_a^2+x_a^2+y_a^2+z_a^2}$$可以驗證，兩個四元數乘積的模即模的乘積，這使得單位四元數相乘後仍是單位四元數：$$\Vert q_a{q}_b\Vert =\Vert q_a\Vert \Vert q_b\Vert$$

4. 共軛
   四元數的共軛是把虛部取成相反數：$$q_a^{\ast }=s_a-x_{a}i-y_{a}j-z_{a}k=[s_a,-v_a].$$四元數共軛與其本身相乘，會得到一個實四元數，其實部為模長的平方：$$q^{\ast }q=q{q}^{\ast }=[s^2+v^{T}v,0{]}^T$$

5. 逆
   一個四元數的逆為：$$q^{-1}=q^{\ast }/\Vert q\Vert$$按此定義，四元數和自己的逆的乘積為實四元數$1$：$$q{q}^{-1}=q^{-1}q=q{q}^{\ast }/{\Vert q\Vert }^2=1$$如果$\mathbf{q}$為單位四元數，其逆和共軛就是同一個量。同時，乘積的逆具有和矩陣相似的性質：$$(q_a{q}_b{)}^{-1}=q_b^{-1}{q}_a^{-1}$$

6. 數乘
   又稱標量乘法，四元數可以與數相乘：$$k\mathbf{q}=[ks,kv{]}^T$$

3. 用四元數表示旋轉

3.1 四元數與旋轉關係

我們可以用四元數表達對一個點的旋轉。假設有一個空間三維點$p=[x,y,z]\in {\mathbb{R}}^3$，以及一個由單位四元數$q$指定的旋轉。三維點$p$經過$q$的旋轉後變為$p^{{}^{\prime }}$。如果使用矩陣描述，那麼有$p^{{}^{\prime }}=Rp$。而如何用四元數描述旋轉呢？
首先，把三維空間點用一個虛四元數來描述：$$w=[0,x,y,z{]}^T=[0,v{]}^T$$相當於把四元數的3個虛部和空間中的3個軸相對應。那麼，旋轉後的點$w^{{}^{\prime }}$可表示為這樣的乘積：$$w^{{}^{\prime }}=qw{q}^{-1}$$這裡的乘法均為四元數乘法，結果也是四元數。最後把$w^{{}^{\prime }}$的虛部取出，即得旋轉之後點的座標。並且可以驗證，計算結果的實部為0，即為虛四元數。
下面從幾何的角度進一步講解四元數與3D旋轉之間的關聯。如果只是簡單應用，不需要了解幾何證明過程，則本小節就足夠了。

3.2 四元數與3D旋轉幾何證明

回憶一下《旋轉向量與羅德里格斯公式》討論的內容：如果我們需要將一個向量$v$沿著一個用單位向量所定義的旋轉軸$u$旋轉$\theta$度，那麼可以將其拆分為正交於旋轉軸的$v_{\perp }$以及平行於旋轉軸的$v_{\parallel }$，進行旋轉後獲得$v_{\perp }^{{}^{\prime }}$和$v_{\parallel }^{{}^{\prime }}$，相加後得到旋轉後的結果$v^{{}^{\prime }}=v_{\perp }^{{}^{\prime }}+v_{\parallel }^{{}^{\prime }}$。
將這些向量定義為純四元數，下表$q$代表對應四元數：
$$\begin{array}{rlrl}& w=[0,v]& & w^{{}^{\prime }}=[0,v^{{}^{\prime }}]\\ & w_{\perp }=[0,v_{\perp }]& & w_{\perp }^{{}^{\prime }}=[0,v_{\perp }^{{}^{\prime }}]\\ & w_{\parallel }=[0,v_{\parallel }]& & w_{\parallel }^{{}^{\prime }}=[0,v_{\parallel }^{{}^{\prime }}]\\ & u_q=[0,u]& & \end{array}$$那麼我們就能得到：$$\begin{array}{rlr}w=w_{\perp }+w_{\parallel }& & w^{{}^{\prime }}=w_{\perp }^{{}^{\prime }}+w_{\parallel }^{{}^{\prime }}\end{array}$$和之前一樣，這裡也分開討論$w_{\perp }$和$w_{\parallel }$的情況。

3.2.1 $w_{\perp }$的旋轉

之前推導過，如果一個向量$v_{\perp }$正交於旋轉軸$u$，那麼$$v_{\perp }^{{}^{\prime }}=cos(\theta )v_{\perp }+sin(\theta )(u\times v_{\perp })$$將三維向量替換為對應的四元數，$v_{\perp }^{{}^{\prime }}$和$v_{\perp }$可以直接替換，而對於$u\times v_{\perp }$，由於$$\begin{array}{rl}w{w}_{\perp }& =[-u\cdot v_{\perp },u\times v_{\perp }]\\ & =[0,u\times v_{\perp }]\\ & =u\times v_{\perp }\end{array}$$將之前定義的四元數帶入，就能得到$$w_{\perp }^{{}^{\prime }}=cos(\theta )w_{\perp }+sin(\theta )(u_q{w}_{\perp })$$因為四元數遵守分配率，可以繼續變換這個等式：$$w_{\perp }^{{}^{\prime }}=(cos(\theta )+sin(\theta )u_q)w_{\perp }$$此時，可以將$cos(\theta )+sin(\theta )u_q$看作一個四元數，記為$q$，且$\Vert q\Vert =1$（讀者可以自證，用到$\Vert u\Vert =1$），這樣我們就能將旋轉寫成四元數的乘積了。到此為止，我們已經將旋轉與四元數的積聯絡起來了，由此得到$$w_{\perp }^{{}^{\prime }}=q{w}_{\perp }$$也就是說，如果旋轉軸$u$的座標為$u=\left[\begin{array}{c}{u}_x\\ u_y\\ u_z\end{array}\right]$，旋轉角為$\theta$，那麼完成這一旋轉所需要的四元數$q$可以構造為：$$\begin{array}{rl}q& =cos(\theta )+sin(\theta )u_q\\ & =[cos(\theta ),0]+[0,sin(\theta )u]\\ & =[cos(\theta ),sin(\theta )u]\\ & =cos(\theta )+sin(\theta )u_{x}i+sin(\theta )u_{y}j+sin(\theta )u_{z}k\end{array}$$總結一下，得到定理3D旋轉公式（正交四元數型）：當$v_{\perp }$正交於旋轉軸$u$時，旋轉$\theta$角度之後的$v_{\perp }^{{}^{\prime }}$可以使用四元數乘法來獲得。令$w_{\perp }=[0,v_{\perp }]$，$q=[cos(\theta ),sin(\theta )u]$，那麼：$$w_{\perp }^{{}^{\prime }}=q{w}_{\perp }$$

3.2.2 $w_{\parallel }$的旋轉

接下來是平行於旋轉軸的$w_{\parallel }$。之前已經討論過，如果一個向量$v_{\parallel }$平行於$u$，那麼旋轉$\theta$後對它不會做出任何變換，由此得到定理3D旋轉公式（平行四元數型）：當$v_{\parallel }$平行於旋轉軸$u$時，旋轉$\theta$角度之後的$v_{\parallel }^{{}^{\prime }}$用四元數可以寫為：$$w_{\parallel }^{{}^{\prime }}=w_{\parallel }$$

3.2.3 $w$的旋轉

有了前面的結論，我們可以獲得一般情況下$w^{{}^{\prime }}$的結果了：$$\begin{array}{rl}{w}^{{}^{\prime }}& =w_{\parallel }^{{}^{\prime }}+w_{\perp }^{{}^{\prime }}\\ & =w_{\parallel }+q{w}_{\perp }\end{array}$$在進一步化簡之前，引入三個引理：

1. 如果$q=[cos(\theta ),sin(\theta )u]$，而且$u$為單位向量，那麼$q^2=qq=[cos(2\theta ),sin(2\theta )u]$。
2. 假設$w_{\parallel }=[0,v_{\parallel }]$是一個純四元數，而$q=[\alpha ,\beta u]$，其中$u$是一個單位向量，$\alpha ,\beta \in \mathbb{R}$。在這種條件下，如果$v_{\parallel }$平行於$u$，那麼$q{v}_{\parallel }=v_{\parallel }q$。
3. 假設$w_{\perp }=[0,v_{\perp }]$是一個純四元數，而$q=[\alpha ,\beta u]$，其中$u$是一個單位向量，$\alpha ,\beta \in \mathbb{R}$。在這種條件下，如果$v_{\perp }$平行於$u$，那麼$q{v}_{\perp }=v_{\perp }{q}^{\ast }$。

關於引理的證明，讀者可以參考文獻2，這裡不再擴充套件。
為方便證明，再引入一個新的四元數$p=[cos(\frac{1}{2}\theta ),sin(\frac{1}{2}\theta )u]$，$q=p^2$，$\Vert p\Vert =1$。現在，我們就能對原本的旋轉公式進行變形了：$$\begin{array}{rl}{w}^{{}^{\prime }}& =w_{\parallel }+q{w}_{\perp }\\ & =p{p}^{-1}{w}_{\parallel }+pp{w}_{\perp }\\ & =p{p}^{\ast }{w}_{\parallel }+pp{w}_{\perp }\\ & =p{w}_{\parallel }{p}^{\ast }+p{w}_{\perp }{p}^{\ast }\\ & =p(w_{\parallel }+w_{\perp })p^{\ast }\\ & =p{w}_{}{p}^{\ast }\end{array}$$至此，我們就解開了四元數與3D旋轉之間的謎題。3D空間中任意一個旋轉都能夠用一個三個四元數相乘的形式表達出來。
綜上，我們可以總結出一個定理3D旋轉公式（一般情況四元數型）：任意向量$v$沿著以單位向量定義的旋轉軸$u$旋轉$\theta$度之後的$v^{{}^{\prime }}$，可以使用四元數乘法來獲得。令$w=[0,v],q=[cos(\frac{1}{2}\theta ),sin(\frac{1}{2}\theta )u]$，那麼：$$w^{{}^{\prime }}=qw{q}^{\ast }=qw{q}^{-1}$$這裡用的是$\frac{1}{2}\theta$而不是$\theta$。這是因為$q$做的就是一個$\frac{1}{2}\theta$的旋轉，而$q^{\ast }$或$q^{-1}$也做了一個$\frac{1}{2}\theta$的旋轉。我們進行了兩次旋轉，而不是一次，這兩次旋轉的結果是一個旋轉角為$\theta$的旋轉。下圖或可解釋旋轉的過程：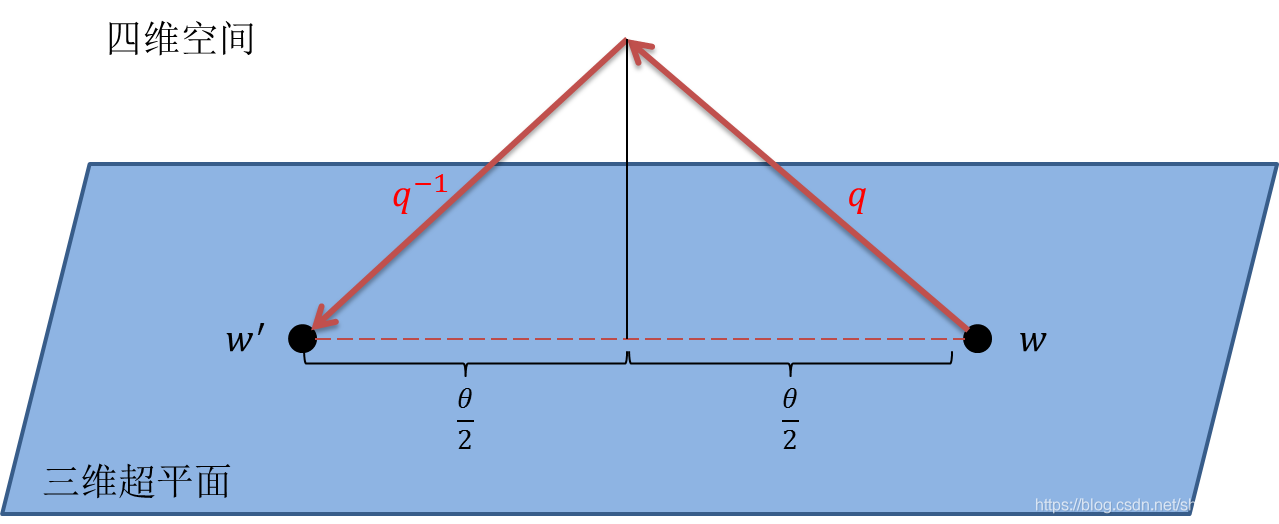
對$w^{{}^{\prime }}=qw{q}^{\ast }=qw{q}^{-1}$，我的理解是：對向量$v$轉化成的純四元數$w$，經過$q$的旋轉$qw$後，得到實部不為0的普通四元數，這時沒辦法對映到三維超平面（總不能轉著圈就轉到了四維空間吧），結果與最初的點不在同一三維空間。為了解決這個問題，先對第四維（角度）旋轉一半，再用逆或共軛旋轉回來，這時正好將產生的第四維變為0，重新回到初始的三維超平面空間。這樣不僅解決了奇點問題，也不會產生冗餘資料，不知道$Hamilton$怎麼想到的，太牛了。

4. 四元數到其它旋轉表示的相互轉換

任意單位四元數描述了一個旋轉，該旋轉也可用旋轉向量、旋轉矩陣或尤拉角描述。現在來考察四元數與旋轉向量、旋轉矩陣或尤拉角的相互轉換關係。

4.1 旋轉向量

本節介紹旋轉向量與四元數之間的轉換關係。
繞座標軸的多次旋轉可以等效為繞某一轉軸旋轉一定的角度。假設已知等效旋轉軸方向單位旋轉向量$u$的座標為$u=\left[\begin{array}{c}{u}_x\\ u_y\\ u_z\end{array}\right]$，旋轉角為$\theta$。根據3.2.3推導的定理3D旋轉公式（一般情況四元數型），設其等效的單位四元數為$q=[q_0,q_1,q_2,q_3]$，則有：$$\{\begin{array}{c}{q}_0=cos(\frac{1}{2}\theta )\\ q_1=u_{x}sin(\frac{1}{2}\theta )\\ q_2=u_{y}sin(\frac{1}{2}\theta )\\ q_3=u_{z}sin(\frac{1}{2}\theta )\end{array}\text{\hspace{1em}(4.1)}$$
同理，當已知單位四元數$q=[q_0,q_1,q_2,q_3]$，其對應的旋轉角$\theta$和旋轉向量$u$為：$$\{\begin{array}{c}\theta =2\arccos q_0\\ [u_x,u_y,u_z{]}^T=[q_1,q_2,q_3{]}^T/\sin (\frac{2}{\theta })\end{array}\text{\hspace{1em}(4.2)}$$

4.2 旋轉矩陣

已知單位四元數$q$，根據博文《三維空間剛體運動2：旋轉向量與羅德里格斯公式》中的羅德里格斯公式展開式（2.3）及本文公式（4.2），將單位旋轉向量$u$及旋轉角$\theta$替換為單位四元數$q$，省去計算過程，得到單位四元數到旋轉矩陣的轉換公式為：$$R=\left[\begin{array}{ccc}1-2q_2^2-2q_3^2& 2(q_1{q}_2-q_0{q}_3)& 2(q_1{q}_3+q_0{q}_2)\\ 2(q_1{q}_2+q_0{q}_3)& 1-2q_1^2-2q_3^2& 2(q_2{q}_3-q_0{q}_1)\\ 2(q_1{q}_3-q_0{q}_2)& 2(q_2{q}_3+q_0{q}_1)& 1-2q_1^2-2q_2^2\end{array}\right]\text{\hspace{1em}(4.3)}$$
假設已知變換矩陣：$$R=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]$$根據公式（4.3），推導對應的單位四元數為：$$\{\begin{array}{c}{q}_0=\frac{1}{2}\sqrt{1+r_{11}+r_{22}+r_{33}}\\ q_1=\frac{r_{32}-r_{23}}{4q_0}\\ q_2=\frac{r_{13}-r_{31}}{4q_0}\\ q_3=\frac{r_{21}-r_{12}}{4q_0}\end{array}\text{\hspace{1em}(4.4)}$$

4.3 尤拉角

那麼將Z-Y-X尤拉角（或RPY角：繞固定座標系的X-Y-Z依次旋轉α,β,γ角）轉換為四元數：$$q=\left[\begin{array}{c}\cos \frac{\gamma }{2}\\ 0\\ 0\\ \sin \frac{\gamma }{2}\end{array}\right]\left[\begin{array}{c}\cos \frac{\beta }{2}\\ 0\\ \sin \frac{\beta }{2}\\ 0\end{array}\right]\left[\begin{array}{c}\cos \frac{\alpha }{2}\\ \sin \frac{\alpha }{2}\\ 0\\ 0\end{array}\right]=\left[\begin{array}{c}\cos \frac{\alpha }{2}\cos \frac{\beta }{2}\cos \frac{\gamma }{2}+\sin \frac{\alpha }{2}\sin \frac{\beta }{2}\sin \frac{\gamma }{2}\\ \sin \frac{\alpha }{2}\cos \frac{\beta }{2}\cos \frac{\gamma }{2}-\cos \frac{\alpha }{2}\sin \frac{\beta }{2}\sin \frac{\gamma }{2}\\ \cos \frac{\alpha }{2}\sin \frac{\beta }{2}\cos \frac{\gamma }{2}+\sin \frac{\alpha }{2}\cos \frac{\beta }{2}\sin \frac{\gamma }{2}\\ \cos \frac{\alpha }{2}\cos \frac{\beta }{2}\sin \frac{\gamma }{2}-\sin \frac{\alpha }{2}\sin \frac{\beta }{2}\cos \frac{\gamma }{2}\end{array}\right]$$
根據上面的公式可以求出逆解，即由四元數$q=(q_0,q_1,q_2,q_3)$到尤拉角的轉換為：$$\left[\begin{array}{c}\alpha \\ \beta \\ \gamma \end{array}\right]=\left[\begin{array}{c}atan2(2(q_0{q}_1+q_2{q}_3),1-2(q_1^2+q_2^2))\\ \arcsin (2(q_0{q}_2-q_1{q}_3)\\ atan2(2(q_0{q}_3+q_1{q}_2),1-2(q_2^2+q_3^2))\end{array}\right]$$這裡使用了$atan2(y,x)$而不是$arctan(\frac{y}{x})$，因為$arctan(\frac{y}{x})$的取值範圍為$[-\frac{\pi }{2},\frac{\pi }{2}]$，只有$180°$，而繞某個軸旋轉時範圍是$360°$，$atan2(y,x)$正好滿足需求。$atan2(y,x)$是一個函數，在C語言裡返回的是指方位角，函數原型為$doubleatan2(doubley,doublex)$ ，返回以弧度表示的 $y/x$ 的反正切。y 和 x 的值的符號決定了正確的象限。也可以理解為計算複數$x+yi$ 的輻角，計算時atan2 比 atan 穩定。
另外需要注意的就是奇異性問題，即萬向鎖，下面分析這種情況。當剛體繞Y軸旋轉了$90°$（俯仰角pitch=90）時，如何計算橫滾角roll和偏航角yaw？這時會發生自由度丟失的情況，即Yaw和Roll會變為一個自由度。此時再使用上面的公式根據四元數計算尤拉角會出現問題：$\arcsin (2(q_0{q}_2-q_1{q}_3)$的定義域為$[-1,1]$，當$2(q_0{q}_2-q_1{q}_3)=\pm 0.5$時（在程式中浮點數不能直接進行等於判斷，要使用合理的閾值），俯仰角$\beta$為$\pm 90°$，將其帶入正向公式計算出四元數$(q_0,q_1,q_2,q_3)$，然後可以發現逆向公式中atan2函數中的引數全部為0，即出現了$\frac{0}{0}$的情況！無法計算。
當$\beta =90°$時，$\sin \frac{\beta }{2}=\cos \frac{\beta }{2}=0.707$，將其帶入公式中有：$$q=\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\end{array}\right]=\left[\begin{array}{c}0.707(\cos \frac{\alpha }{2}\cos \frac{\gamma }{2}+\sin \frac{\alpha }{2}\sin \frac{\gamma }{2})\\ 0.707(\sin \frac{\alpha }{2}\cos \frac{\gamma }{2}-\cos \frac{\alpha }{2}\sin \frac{\gamma }{2})\\ 0.707(\cos \frac{\alpha }{2}\cos \frac{\gamma }{2}+\sin \frac{\alpha }{2}\sin \frac{\gamma }{2})\\ 0.707(\cos \frac{\alpha }{2}\sin \frac{\gamma }{2}-\sin \frac{\alpha }{2}\cos \frac{\gamma }{2})\end{array}\right]=\left[\begin{array}{c}0.707\cos \frac{\alpha -\gamma }{2}\\ 0.707\sin \frac{\alpha -\gamma }{2}\\ 0.707\cos \frac{\alpha -\gamma }{2}\\ -0.707\sin \frac{\alpha -\gamma }{2}\end{array}\right]$$則$\frac{q_1}{q_0}=-\frac{q_3}{q_2}=\tan \frac{\alpha -\gamma }{2}$，於是有：$$\alpha -\gamma =2atan2(q_1,q_0)$$通常令$\alpha =0$，這時$\gamma =-2atan2(q_1,q_0)$。當俯仰角為-90°，即剛體豎直向下時的情況也與之類似，可以推匯出奇異姿態時的計算公式。
將四元數轉換為尤拉角可以參考附件。需要注意尤拉角有12種旋轉次序，而上面推導的公式是按照Z-Y-X順序進行的，所以有時會在網上看到不同的轉換公式（因為對應著不同的旋轉次序），在使用時一定要注意旋轉次序是什麼。比如ADAMS軟體裡就預設Body 3-1-3次序，即Z-X-Z尤拉角，而VREP中則按照X-Y-Z尤拉角旋轉。另外萬向鎖問題程式碼的Z-Y-X尤拉角程式碼見類CameraSpacePoint。

5. 四元數的其他性質

為更全面理解四元數和方便引入slerp插值，這一節補充四元數的其它性質：旋轉複合、雙倍覆蓋和指數形式。

5.1 旋轉的複合

旋轉的複合其實在我們之前證明$q^2=qq=[cos(2\theta ),sin(2\theta )u]$的時候就已經涉及到一點了，但是這裡我們考慮的是更一般的情況。
假設有兩個表示沿著不同軸、不同角度旋轉的四元數$q_1、q_2$。首先，我們實施 $q_1$的變換，變換之後的$v^{{}^{\prime }}$為$$v^{{}^{\prime }}=q_{1}v{q}_1^{\ast }$$接下來，對$v^{{}^{\prime }}$進行$q_2$的變換，得到$v^{{}^{\prime \prime }}$：$$v^{{}^{\prime \prime }}=q_2{v}^{{}^{\prime }}{q}_2^{\ast }=q_2{q}_{1}v{q}_1^{\ast }{q}_2^{\ast }=q_{net}v{q}_{net}^{\ast }$$其中$q_{net}=q_2{q}_1$，另外寫成上面的形式，還用到性質$q_1^{\ast }{q}_2^{\ast }=(q_2{q}_1{)}^{\ast }$。
注意四元數乘法的順序，這和矩陣、複數的複合非常相似，都是從右往左疊加。另外要注意的是，$q_1$與$q_2$的等價旋轉$q_{net}$並不是沿著q_{1}$與$q_{2}$的兩個旋轉軸進行的兩次旋轉，它是沿著一個全新的旋轉軸進行的一個等價旋轉，僅僅只有旋轉的結果相同。

5.2 雙倍覆蓋

四元數與 3D 旋轉的關係並不是一對一的，同一個 3D 旋轉可以使用兩個不同的四元數來表示．對任意的單位四元數$q=[cos(\frac{1}{2}\theta ),sin(\frac{1}{2}\theta )u]$，$q$與$-q$代表的是同一個旋轉。如果$q$表示的是沿著旋轉軸$u$旋轉$\theta$度，那麼$-q$代表的是沿著相反的旋轉軸$-u$旋轉$(2\pi -\theta )$，負負得正：$$\begin{array}{rl}-q& =[-cos(\frac{1}{2}\theta ),-sin(\frac{1}{2}\theta )u]\\ & =[cos(\pi -\frac{1}{2}\theta ),sin(\pi -\frac{1}{2}\theta )(-u)]\end{array}$$所以，這個四元數旋轉的角度為$2(\pi -\frac{1}{2}\theta )=2\pi -\theta$，從下面的圖中我們可以看到，這兩個旋轉是完全等價的：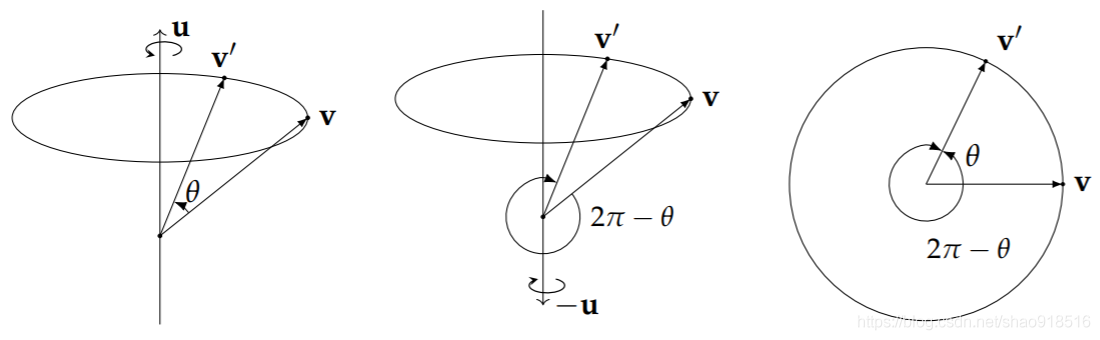
其實從四元數的旋轉公式中也能推匯出相同的結果：$$(-q)v(-q{)}^{\ast }=(-1{)}^{2}qv{q}^{\ast }=qv{q}^{\ast }$$所以，我們經常說單位四元數與3D旋轉有一個「2對1滿射同態」(2-1 Surjective Homomorphism) 關係，或者說單位四元數雙倍覆蓋(Double Cover)了3D旋轉。它的嚴格證明會用到一些李群的指示，這裡不再拓展。
有一點需要注意的是，雖然$q$與$-q$是兩個不同的四元數，但是由於旋轉矩陣中的每一項都包含了四元數兩個分量的乘積，它們的旋轉矩陣是完全相同的，即旋轉矩陣並不會出現雙倍覆蓋的問題。

5.3 指數形式

在討論複數的時候，我們利用尤拉公式將2D的旋轉寫成了$v^{{}^{\prime }}=e^{i\theta v}$這樣的指數形式。實際上，我們也可以利用四元數將 3D 旋轉寫成類似的形式。
類似於複數的尤拉公式，四元數也有一個類似的公式。如果$u$是一個單位向量，那麼對於單位四元數$u_q=[0,u]$，有：$$e^{u\theta }=cos(\theta )+u_{q}sin(\theta )=cos(\theta )+usin(\theta )$$這也就是說，$q=[cos(\theta ),sin(\theta )u]$可以使用指數表示為$e^{u\theta }$。這個公式的證明與尤拉公式的證明非常類似，直接使用級數展開就可以了，這裡不再擴充套件。
注意，因為$u$是一個單位向量，$u^2=[-u\cdot u,0]=-\Vert u{\Vert }^2=-1$．這與尤拉公式中的$i$是非常類似的。有了指數型的表示方式，我們就能夠將之前四元數的旋轉公式改寫為指數形式了，由此可得到定義：
3D旋轉公式（指數型）：任意向量$v$沿著以單位向量定義的旋轉軸$u$旋轉$\theta$角度之後的$v^{{}^{\prime }}$可以使用四元數的指數表示．令$w=[0,v],u_q=[0,u]$，那麼：$$w=e^{u_q\frac{\theta }{2}}v{e}^{-u_q\frac{\theta }{2}}$$有了四元數的指數定義，我們就能夠定義四元數的更多運算了。首先是自然對數$log$，對任意單位四元數$q=[cos(\theta ),sin(\theta )u]=e^{u_q\theta }$：$$log(q)=log(e^{u_q\theta })=[0,u\theta ]$$接下來是單位四元數的冪運算：$$q^t=(e^{u_q\theta }{)}^t=e^{u_q(t\theta )}=[cos(t\theta ),sin(t\theta )u]$$可以看到，一個單位四元數的$t$次冪等同於將它的旋轉角度縮放至$t$倍，並且不會改變它的旋轉軸（$u$必須是單位向量，所以一般不能與$t$結合）。這些運算會在之後討論四元數插值時非常有用。限於篇幅，四元數插值的講解見下一篇部落格《三維空間剛體運動4-2：四元數插值（lerp，Nlerp，Slerp，Squad等）》

6. 實踐

現在，我們通過兩個小程式實際演練四元數的運算。

6.1 四元數常規運算

第一個小程式是演示四元數的常規運算，包括與旋轉矩陣和旋轉向量的轉換，以及用四元數旋轉一個向量，如下所示：

#include<iostream>
#include<cmath>
using namespace std;

#include<eigen3/Eigen/Core>
#include<eigen3/Eigen/Geometry>

using namespace Eigen;

int main(int argc, char **argv){
    //Eigen/Geometry模組提供了各種旋轉和平移的表示，3D旋轉矩陣直接使用Matrix3d或Matrix3f
    Matrix3d rotation_matrix = Matrix3d::Identity();
    //旋轉向量使用AngleAxis，它底層不直接是Matrix，但運算可以當做矩陣，因為過載了運運算元
    AngleAxisd rotation_vector(M_PI/4, Vector3d(0, 0, 1));
    //設定輸出精度
    cout.precision(3);
    cout<<"rotation matrix =\n"<<rotation_matrix<<endl;
    cout<<"rotation vector =\n"<<rotation_vector.matrix()<<endl;
    
    //旋轉向量轉換的矩陣可以直接賦值給旋轉矩陣
    rotation_matrix = rotation_vector.toRotationMatrix();
    cout<<"rotation vector to Matrix =\n"<<rotation_matrix<<endl;
    
    //旋轉向量
    Vector3d v(1, 0, 0);
    cout<<"v = "<<v.transpose()<<endl;
    
	//四元數，可以直接把AngleAxis賦值給四元數，反之亦然
    Quaterniond q = Quaterniond(rotation_vector);
    //coeffs:多項式係數（coefficients)，其順序為(x,y,z,w)，w為實部，xyz為虛部
    cout<<"quaternion from rotation vector = "<<q.coeffs().transpose()<<endl;
    //也可以直接把旋轉矩陣賦給它
    q = Quaterniond(rotation_matrix);
    cout<<"quaternion from rotation matrix = "<<q.coeffs().transpose()<<endl;
    //使用四元數旋轉一個向量，使用過載的乘法即可
    //注意q*v在數學上是qvq^{-1}
    v_rotated = q*v;
    cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;
    //用常規向量乘法表示qvq^{-1}，則計算如下：
    Quaterniond q_rotate_v = q*Quaterniond(0,1,0,0)*q.inverse();
    cout<<"should be equal to "<<q_rotate_v.coeffs().transpose()<<endl;
    
    return 0;

輸出結果如下：

rotation matrix =
1 0 0
0 1 0
0 0 1
rotation vector =
 0.707 -0.707      0
 0.707  0.707      0
     0      0      1
rotation vector to Matrix =
 0.707 -0.707      0
 0.707  0.707      0
     0      0      1
v = 1 0 0
v transofrmed = 1.71 3.71    4
quaternion from rotation vector =     0     0 0.383 0.924
quaternion from rotation matrix =     0     0 0.383 0.924
(1,0,0) after rotation = 0.707 0.707     0
should be equal to 0.707 0.707     0     0

請讀者注意，程式程式碼通常和數學表示有一些細微的差別。例如，通過運運算元過載，四元數和三維向量可以直接計算乘法，但在數學上則需要先把向量轉成虛四元數，再利用四元數乘法進行計算，同樣的情況也適用於變換矩陣乘三維向量的情況。總體而言，程式中的用法會比數學公式更靈活。

6.2 座標變換

下面我們舉一個小例子來演示座標變換。
例子：設有小蘿蔔一號和小蘿蔔二號位於世界座標系中。記世界座標系為$W$，小蘿蔔們的座標系分別為$R_1$和$R_2$。小蘿蔔一號的位姿為$q_1=[0.35,0.2,0.3,0.1{]}^T$，$t_1=[0.3,0.1,0.1{]}^T$。小蘿蔔二號的位姿為$q_2=[-0.5,0.4,-0.1,0.2{]}^T$，$t_2=[-0.1,0.5,0.3{]}^T$。這裡的$q$和$t$表達的是$T_{R_k,W},k=1,2$，也就是世界座標系到相機座標系的變換關係。現在，小蘿蔔一號看到某個點在自身的座標系下座標為$p_{R_1}=[0.5,0,0.2{]}^T$，求該向量在小蘿蔔二號座標系下的座標。
這是一個非常簡單，但又具有代表性的例子。在實際場景中你經常需要在同一個機器人的不同部分，或者不同機器人之間轉換座標。計算過程也很簡單，只需計算：$$p_{R_2}=T_{R_2,W}{T}_{W,R_1}{p}_{R_1}$$下面請看程式：

#include<iostream>
#include<vector>
#include<algorithm>
#include<eigen3/Eigen/Core>
#include<eigen3/Eigen/Geometry>

using namespace std;
using namespace Eigen;

int main(int argc, char** argv){
    //位姿四元數q1,q2
    Quaterniond q1(0.35, 0.2, 0.3, 0.1), q2(-0.5, 0.4, -0.1, 0.2);
    cout<<"q1.coeffs=\n"<<q1.coeffs()<<endl;
    cout<<"q2.coeffs=\n"<<q2.coeffs()<<endl;
    
    //四元數轉換為旋轉矩陣
    cout<<"q1.matrix=\n"<<q1.matrix()<<endl;
    cout<<"q2.matrix=\n"<<q2.matrix()<<endl;
    //歸一化，轉換為單位四元數
    q1.normalize();
    q2.normalize();
    cout<<"q1.normalize="<<q1.matrix()<<endl;
    cout<<"q2.normalize="<<q2.matrix()<<endl;
    //位移向量t1,t2,小蘿蔔一號下的座標pr1
    Vector3d t1(0.3, 0.1, 0.1), t2(-0.1, 0.5, 0.3);
    Vector3d pr1(0.5, 0, 0.2);
    
    //Eigen::Isometry3d:歐式變換矩陣4*4
    Isometry3d Twr1(q1), Tr2w(q2);
    cout<<"Twr1.matrix="<<Twr1.matrix()<<endl;
    cout<<"Tr2w.matrix="<<Tr2w.matrix()<<endl;
    //座標轉換，計算T=Ra+t
    Twr1.pretranslate(t1);
    Tr2w.pretranslate(t2);
    
    //先將pr1轉換為世界座標系，然後轉換為小蘿蔔二號下的座標pr2
    Vector3d pr2 = Tr2w * Twr1.inverse()*pr1;
    cout<<"pr2.transpose="<<pr2.transpose()<<endl;
    
    return 0;
}

輸出結果如下：

q1.coeffs=
 0.2
 0.3
 0.1
0.35
q2.coeffs=
 0.4
-0.1
 0.2
-0.5
q1.matrix=
  0.8  0.05  0.25
 0.19   0.9 -0.08
-0.17   0.2  0.74
q2.matrix=
  0.9  0.12  0.26
-0.28   0.6  0.36
 0.06 -0.44  0.66
q1.normalize=
  0.238095   0.190476   0.952381
   0.72381   0.619048  -0.304762
 -0.647619   0.761905 0.00952381
q2.normalize=
 0.782609   0.26087  0.565217
-0.608696  0.130435  0.782609
 0.130435 -0.956522   0.26087
Twr1.matrix=
  0.238095   0.190476   0.952381          0
   0.72381   0.619048  -0.304762          0
 -0.647619   0.761905 0.00952381          0
         0          0          0          1
Tr2w.matrix=
 0.782609   0.26087  0.565217         0
-0.608696  0.130435  0.782609         0
 0.130435 -0.956522   0.26087         0
        0         0         0         1
pr2.transpose=
-0.0309731    0.73499   0.296108

四元數的第一部分講解到此，千萬別忘了一鍵三連哦（點贊收藏轉發）。

參考文獻：

1. 《視覺SLAM十四講：從理論到實踐》，高翔、張濤等著，中國工信出版社
2. 四元數與三維旋轉
3. 四元數與尤拉角（RPY角）的相互轉換
4. 如何形象地理解四元數？