【資料結構——樹和二元樹】

一、樹和二元樹的定義

（一）樹的定義

樹是n個結點的有限集，它或為空樹（n=0）;或為非空樹

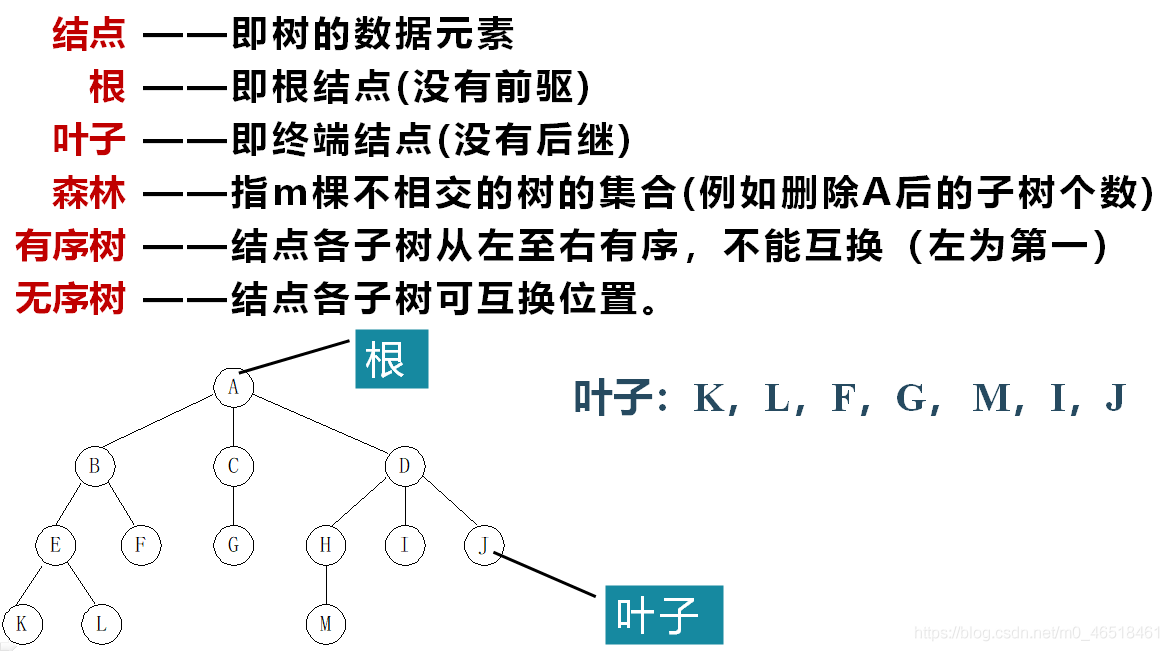
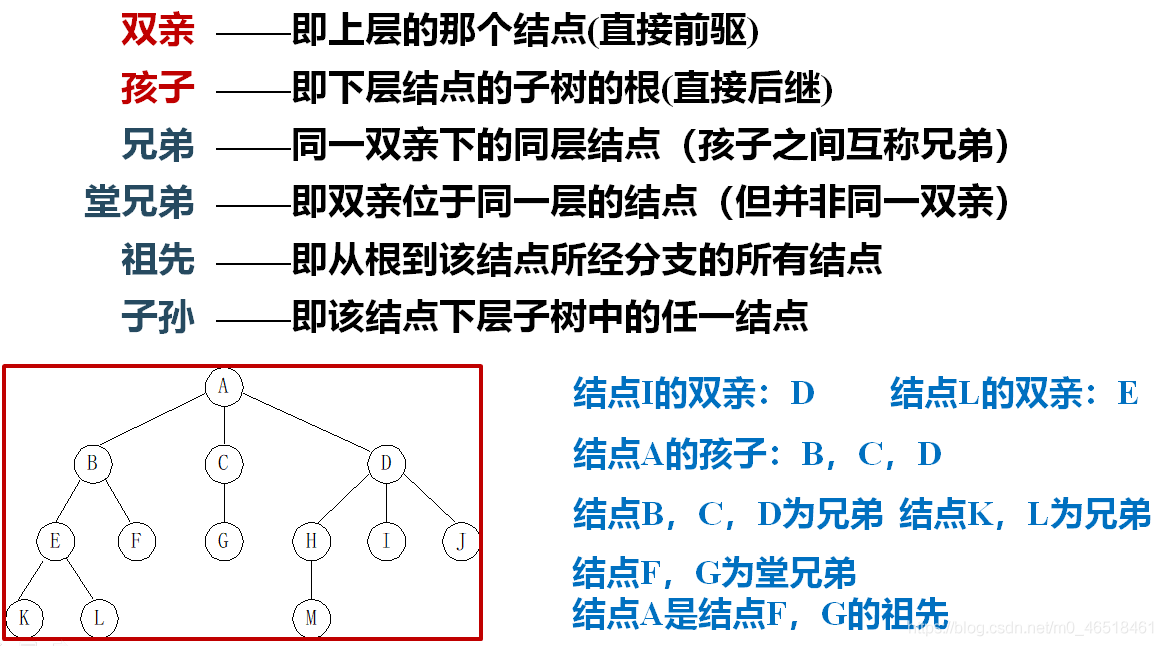
（二）基本術語

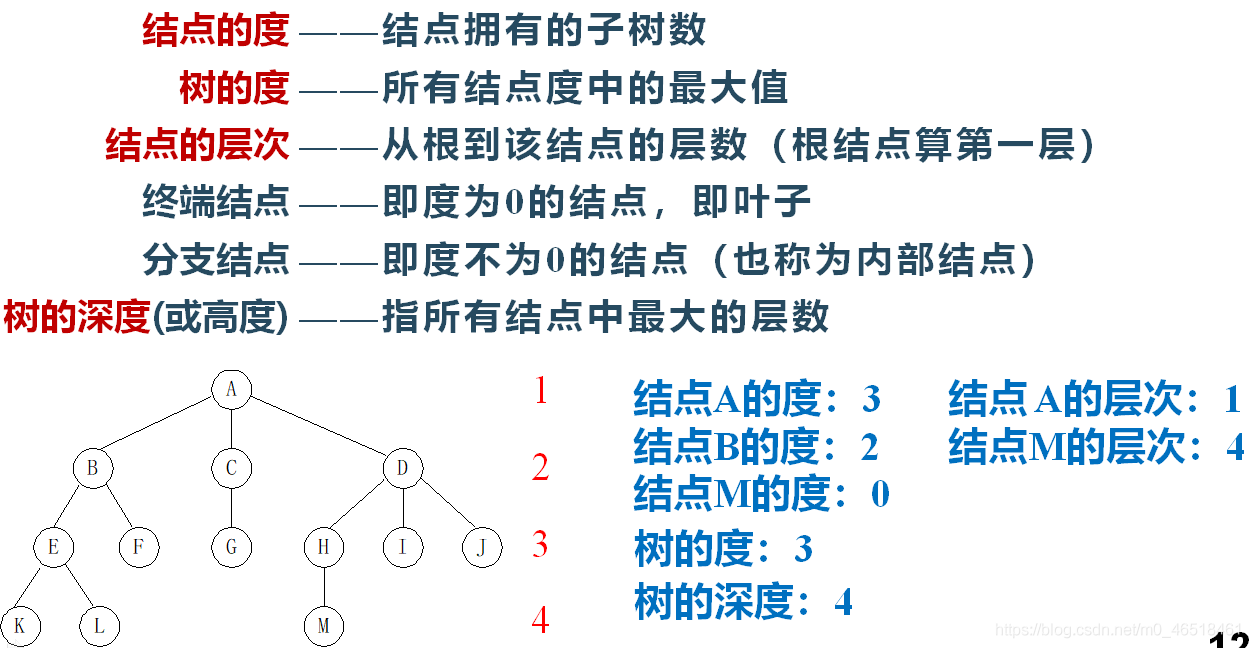
（三）二元樹的定義

1、二元樹的定義

二元樹是n（n>=0）個結點所構成的集合，他或為空樹（n=0）,或為非空樹，對於非空樹：T
（1）有且只有一個稱之為根的結點；
（2）除根結點之外的其餘結點分為兩個互不相交的子集T1和T2，分別稱為T的左子樹和右子樹，且T1和T2本身都是二元樹。

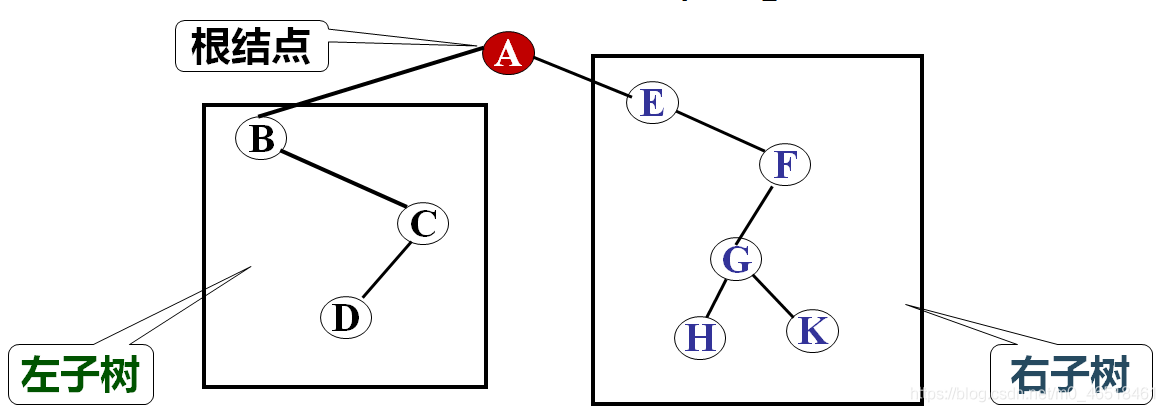
2、二元樹的基本特點

（1）結點的度小於等於2；
（2）有序樹（子樹有左右之分，且其次序不能任意顛倒）

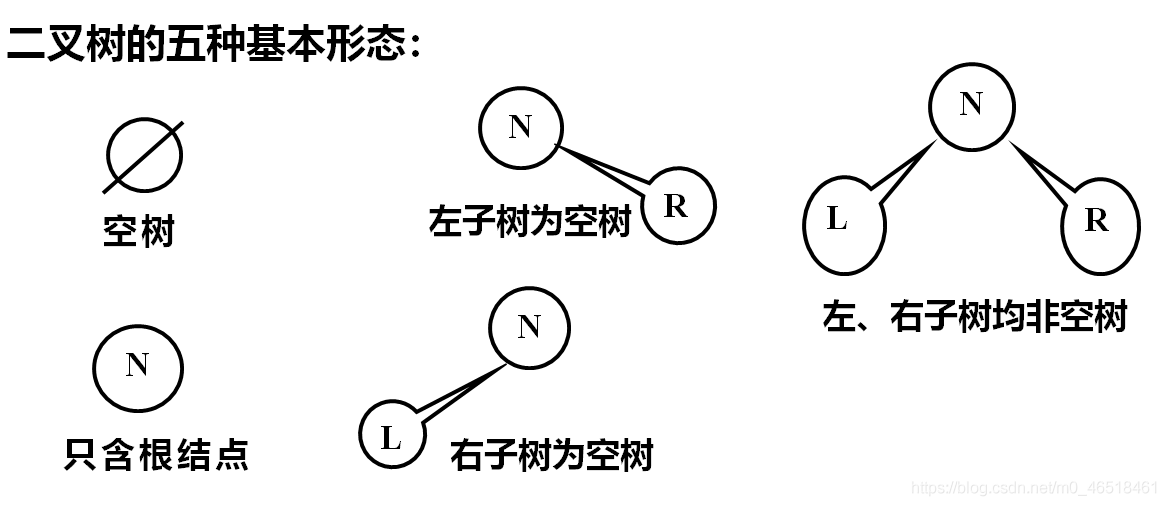
二、二元樹的性質和儲存結構

（一）二元樹的性質

滿二元樹：一棵深度為K且有2的K次方-1個結點的二元樹。（特點：每層都充滿了結點）

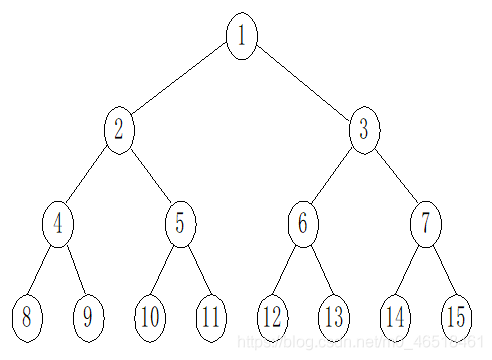
完全二元樹：深度為K的，有n個結點的二元樹，當且僅當其每一個結點都與深度為K的滿二元樹中編號從1至n的結點一一對應。

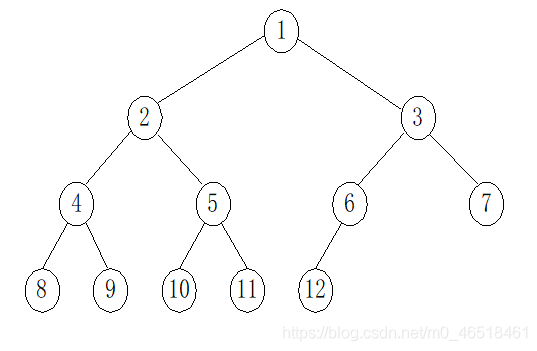
（二）二元樹的儲存結構

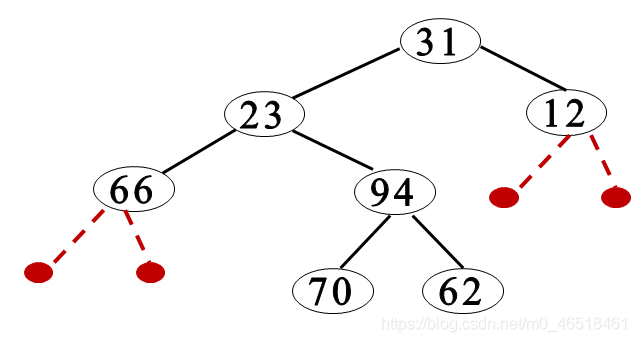
1、順序儲存結構

實現：按完全二元樹的結點層次編號，依次存放二元樹中的資料元素。
特點：
（1）結點間關係蘊含在其儲存位置中；
（2）浪費空間，適於存滿二元樹和完全二元樹。

結點i:
雙親結點：【i/2】
左兒子：2i
右兒子：2i + 1

#define MAXTSIZE 100   //二元樹的最大結點數
typedef TElemType SqBiTree[MAXTSIZE];//0號單元儲存根結點
SqBiTree bt;

2、鏈式儲存結構

（1）二元連結串列

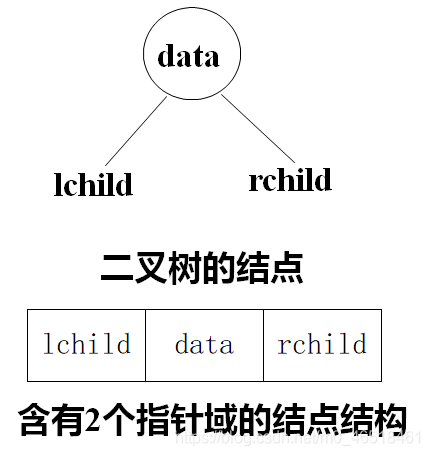
typedef struct BiNode
{
	TElemType data;   //資料域
	struct BiNode* lchild, * rchild;   //左右孩子指標
}BiNode,*BiTree;   //二元樹結點
BiTree root;

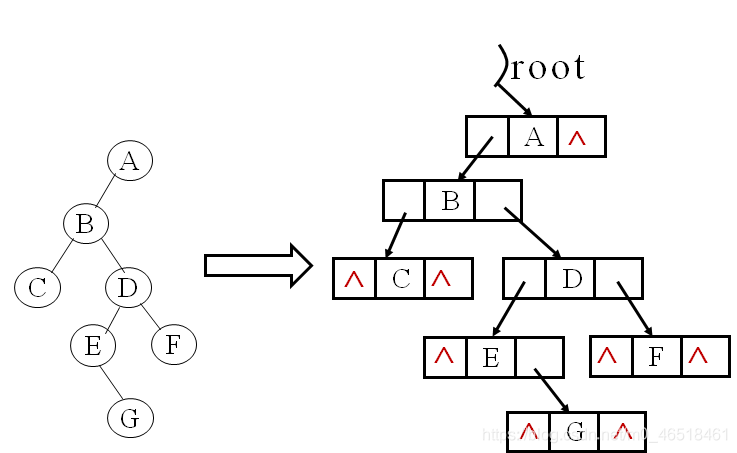
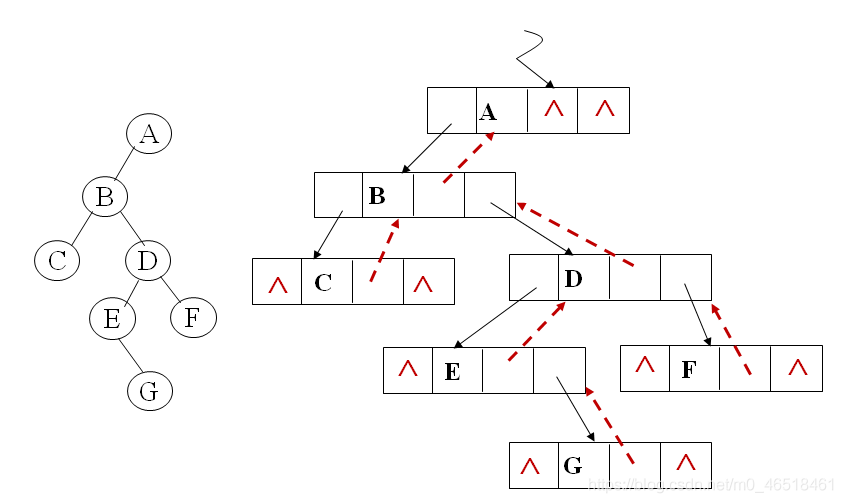
在n個結點的二元連結串列中，有n+1個空指標域

（2）三元連結串列

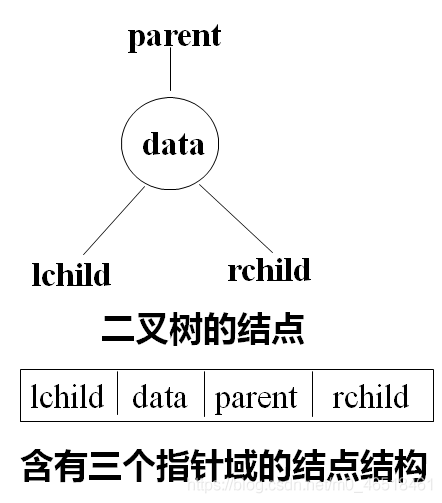
typedef struct TriTNode
{
	TElemType data;   //資料域
	struct TriTNode* lchild,* parent * rchild;   //左右孩子指標
}TriTNode,*TriTree;   //二元樹結點