【閱讀筆記】神經網路中的LRP及其在非線性神經網路中的運用
Layer-Wise Relevance Propagation for Neural Networks with Local Renormalization Layers主要介紹了一種將LRP擴充套件到非線性神經網路的方法。LRP是從模型輸出開始,反向傳播,直到模型輸入開始為止,對由輸入特徵導致其預測結果的解釋,文章中主要探究圖片畫素點與最終結果的相關性。
- 神經網路中的LRP(Layer-Wise Relevance Propagation)
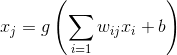
式中 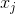 是神經元
是神經元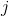 的輸出,
的輸出,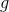 是神經元
是神經元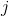 的啟用函數,
的啟用函數,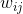 是神經元
是神經元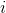 到神經元
到神經元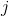 的連線權重,
的連線權重,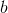 為連線偏差;
為連線偏差;
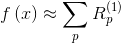
式中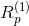 (pixel-wise relevance score) 用於衡量畫素點對預測結果的影響,
(pixel-wise relevance score) 用於衡量畫素點對預測結果的影響,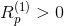 表示某類在圖片中存在的證據,
表示某類在圖片中存在的證據,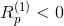 表示某類在圖片中不存在的證據,
表示某類在圖片中不存在的證據,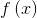 表示對圖片
表示對圖片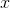 的預測結果,預測結果可視為每個畫素點對應
的預測結果,預測結果可視為每個畫素點對應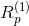 的總和。找出圖片
的總和。找出圖片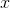 中所有畫素點的
中所有畫素點的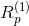 可將圖片
可將圖片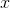 視覺化為熱圖,如下:
視覺化為熱圖,如下:

(圖片1)
假設已知第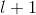 層神經元
層神經元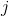 的相關性
的相關性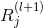 ,可將該相關性
,可將該相關性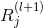 分解到第
分解到第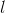 層的所有神經元上,公式如下:
層的所有神經元上,公式如下:
第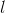 層神經元
層神經元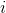 的相關性
的相關性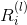 可理解為,第
可理解為,第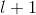 層中所有神經元的相關性分解後再進行求和,公式如下:
層中所有神經元的相關性分解後再進行求和,公式如下:
LRP傳播機制範例如如下,有助於理解上述兩個公式。

(圖片2)LRP傳播機制範例圖
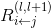 計算方式有兩種:
計算方式有兩種: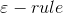 與
與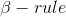
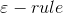 如下:
如下:
式中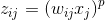 ,
,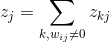 ,筆者認為文章中給出的
,筆者認為文章中給出的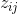 不是很好理解,稍作修改後如下:
不是很好理解,稍作修改後如下:
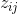 為第
為第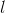 層神經元
層神經元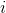 對第
對第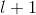 層神經元
層神經元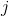 的加權啟用,
的加權啟用,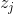 為第
為第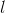 層所有神經元對第
層所有神經元對第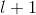 層神經元
層神經元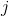 的加權啟用。
的加權啟用。
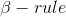 如下:
如下:
式中「+」與「- 」分別表示正值部分與負值部分,即上述公式將正負加權啟用分開進行處理。
」分別表示正值部分與負值部分,即上述公式將正負加權啟用分開進行處理。
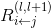 含義如下:
含義如下:
若第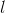 層某個神經元
層某個神經元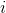 對第
對第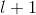 層神經元的一個神經元
層神經元的一個神經元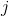 做出了主要貢獻,那麼第
做出了主要貢獻,那麼第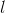 層神經元
層神經元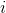 應該佔第
應該佔第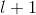 層神經元
層神經元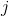 的相關性
的相關性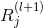 的較大份額,即神經元
的較大份額,即神經元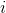 收集它對後一層所連線的神經元
收集它對後一層所連線的神經元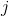 的貢獻。
的貢獻。
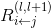 的兩種計算方法
的兩種計算方法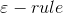 與
與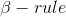 實際上都是將第
實際上都是將第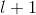 層神經元
層神經元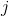 的相關性
的相關性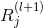 按照比例分配給第
按照比例分配給第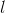 層神經元
層神經元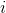 從而求得相關係數
從而求得相關係數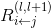 ,因此在LRP中,存在以下的結構:
,因此在LRP中,存在以下的結構:
with
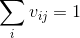
式中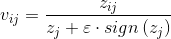 或
或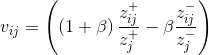 ,對於
,對於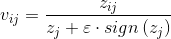 ,筆者認為應該是
,筆者認為應該是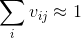 ,因為式中的
,因為式中的 是一個較小的實數。
是一個較小的實數。
- 將LRP運用到非線性神經網路
先考慮一種情況:神經元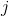 的輸出無法用等式
的輸出無法用等式 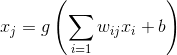 表示,設神經元
表示,設神經元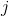 的輸出為
的輸出為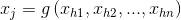 ,式中
,式中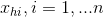 表示神經元
表示神經元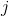 前一層神經元對神經元
前一層神經元對神經元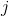 的輸入,現將
的輸入,現將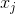 在參考點
在參考點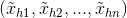 處進行一階泰勒展開得如下式子:
處進行一階泰勒展開得如下式子:
前一層神經元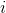 對後一層神經元
對後一層神經元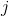 的加權啟用如下:
的加權啟用如下:
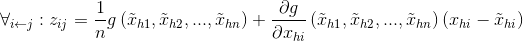
上式可理解為,將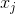 泰勒分解中的零階項平均分配後,再加上前一層對應神經元
泰勒分解中的零階項平均分配後,再加上前一層對應神經元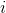 輸入的偏導值,即為前一層神經元
輸入的偏導值,即為前一層神經元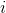 對後一層神經元
對後一層神經元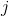 的加權啟用。按照泰勒分解求得
的加權啟用。按照泰勒分解求得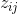 後,可利用本文上述所介紹的
後,可利用本文上述所介紹的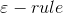 或者
或者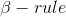 進行逐層相關性的求解,最終可計算出
進行逐層相關性的求解,最終可計算出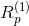 (pixel-wise relevance score)。
(pixel-wise relevance score)。
- 將LRP運用到Local Renormalization Layers
因Local Renormalization Layers在深度神經網路中表現出了良好的效能,所以在這裡介紹將LRP運用到Local Renormalization Layers中,使其具有可解釋性。
將神經網路中某一層設定為Local Renormalization Layers,該層中神經元定義如下:
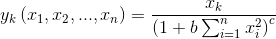
顯然,Local Renormalization Layers為非線性,可將LRP運用到非線性神經網路的方法應用到此處。
將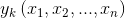 在參考點
在參考點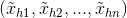 處進行泰勒展開可得如下式子:
處進行泰勒展開可得如下式子:
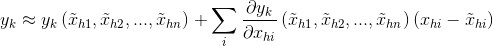
對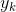 求偏導,如下:
求偏導,如下:
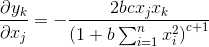 ,此處
,此處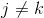
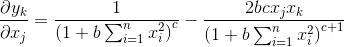 ,此處
,此處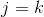
將上面兩個式中,稍作整理可得,
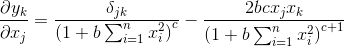
對於輸出為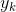 的神經元來說,其輸入應該是
的神經元來說,其輸入應該是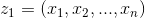 ,若只有輸出為
,若只有輸出為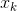 的神經元觸發輸出為
的神經元觸發輸出為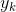 的神經元時,其輸入應該是
的神經元時,其輸入應該是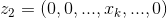 ,即對於輸出為
,即對於輸出為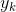 的神經元,我們選擇在只有輸出為
的神經元,我們選擇在只有輸出為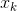 的神經元觸發輸出為
的神經元觸發輸出為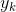 的神經元時候展開,即在點
的神經元時候展開,即在點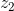 展開,如下:
展開,如下:
上式則意味著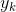 的泰勒一階展開式中一階項對於
的泰勒一階展開式中一階項對於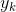 的近似沒有貢獻值,這是我們不希望看到的,故稍作修改,如下:
的近似沒有貢獻值,這是我們不希望看到的,故稍作修改,如下:
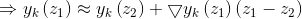
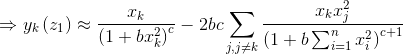
然後根據求得的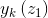 可通過如下式子計算前一層神經元
可通過如下式子計算前一層神經元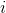 對後一層神經元
對後一層神經元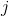 的加權啟用
的加權啟用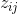 ,
,
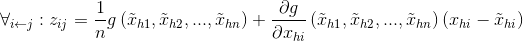
最後可利用本文在最前面所介紹的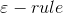 或者
或者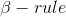 進行逐層相關性的求解,最終可計算出
進行逐層相關性的求解,最終可計算出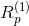 (pixel-wise relevance score)。
(pixel-wise relevance score)。
筆者水平有限,難免存在理解不當之處,歡迎批評指正,聯絡郵箱:changhao1997@foxmail.com
- 參考文獻
- Layer-Wise Relevance Propagation for Neural Networks with Local Renormalization Layers
- 趙新傑. 深度神經網路的視覺化理解方法研究[D].哈爾濱工程大學,2018.
- 陳珂銳,孟小峰.機器學習的可解釋性[J].計算機研究與發展,2020,57(09):1971-1986.