Android自定義控制元件進階09-控制元件核心Matrix原理

本篇的主角Matrix，是一個一直在後台默默工作的勞動模範，雖然我們所有看到View背後都有着Matrix的功勞，但我們卻很少見到它，本篇我們就看看它是何方神聖吧。

由於Google已經對這一部分已經做了很好的封裝，所以跳過本部分對實際開發影響並不會太大，不想深究的粗略瀏覽即可，下一篇中將會詳細講解Matrix的具體用法和技巧。

⚠️ 警告：測試本文章範例之前請關閉硬體加速。

Matrix簡介

Matrix是一個矩陣，主要功能是座標對映，數值轉換。

它看起來大概是下面下麪這樣:

$\left [ \begin{matrix} MSCALE_X & MSKEW_X & MTRANS_X \MSKEW_Y & MSCALE_Y & MTRANS_Y \MPERSP_0 & MPERSP_1 & MPERSP_2 \end{1} \right ]$

Matrix作用就是座標對映，那麼爲什麼需要Matrix呢? 舉一個簡單的例子:

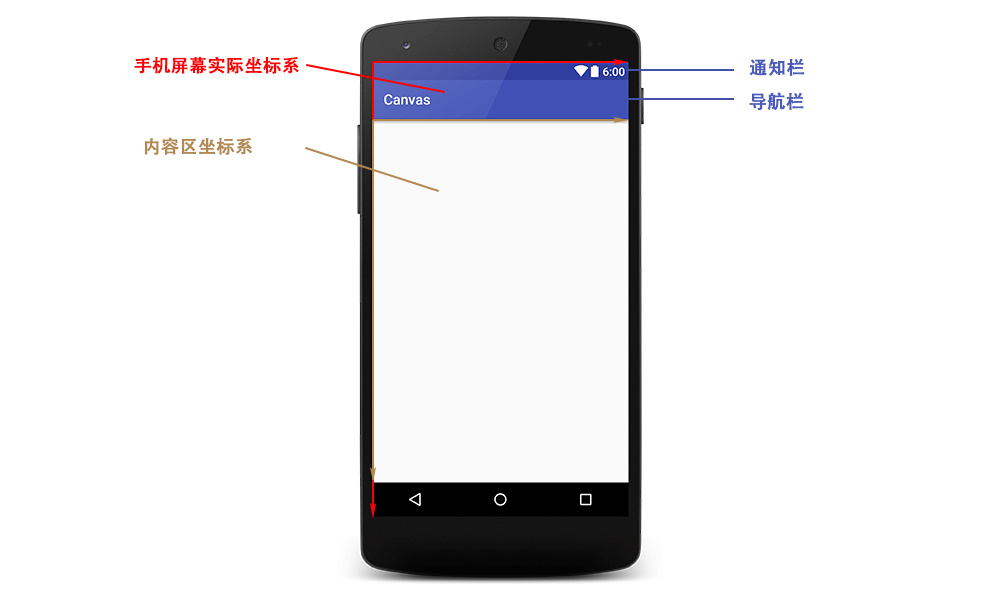
我的的手機螢幕作爲物理裝置，其物理座標系是從左上角開始的，但我們在開發的時候通常不會使用這一座標系，而是使用內容區的座標系。

以下圖爲例，我們的內容區和螢幕座標系還相差一個通知欄加一個標題列的距離，所以兩者是不重合的，我們在內容區的座標系中的內容最終繪製的時候肯定要轉換爲實際的物理座標系來繪製，Matrix在此處的作用就是轉換這些數值。

假設通知欄高度爲20畫素，導航欄高度爲40畫素,那麼我們在內容區的(0，0)位置繪製一個點，最終就要轉化爲在實際座標系中的(0，60)位置繪製一個點。

以上是僅作爲一個簡單的範例，實際上不論2D還是3D，我們要將圖形顯示在螢幕上，都離不開Matrix，所以說Matrix是一個在背後辛勤工作的勞模。

Matrix特點

作用範圍更廣，Matrix在View，圖片，動畫效果等各個方面均有運用，相比與之前講解等畫布操作應用範圍更廣。
更加靈活，畫布操作是對Matrix的封裝，Matrix作爲更接近底層的東西，必然要比畫布操作更加靈活。
封裝很好，Matrix本身對各個方法就做了很好的封裝，讓開發者可以很方便的操作Matrix。
難以深入理解，很難理解中各個數值的意義，以及操作規律，如果不瞭解矩陣，也很難理解前乘，後乘。

常見誤解

1.認爲Matrix最下面下麪的一行的三個參數(MPERSP_0、MPERSP_1、MPERSP_2)沒有什麼太大的作用，在這裏只是爲了湊數。

實際上最後一行參數在3D變換中有着至關重要的作用，這一點會在後面中Camera一文中詳細介紹。

2.最後一個參數MPERSP_2被解釋爲scale

的確，更改MPERSP_2的值能夠達到類似縮放的效果，但這是因爲齊次座標的緣故，並非這個參數的實際功能。

Matrix基本原理

Matrix 是一個矩陣，最根本的作用就是座標轉換，下面下麪我們就看看幾種常見變換的原理:

我們所用到的變換均屬於仿射變換，仿射變換是線性變換(縮放，旋轉，錯切) 和平移變換(平移) 的複合，由於這些概唸對於我們作用並不大，此處不過多介紹，有興趣可自行瞭解。

基本變換有4種: 平移(translate)、縮放(scale)、旋轉(rotate) 和錯切(skew)。

下面下麪我們看一下四種變換都是由哪些參數控制的。

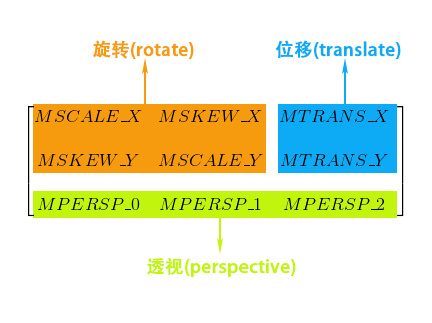
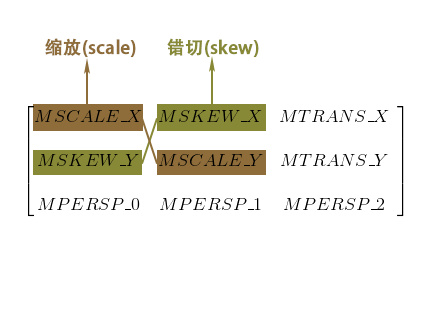
從上圖可以看到最後三個參數是控制透視的，這三個參數主要在3D效果中運用，通常爲(0, 0, 1)，不在本篇討論範圍內，暫不過多敘述，會在之後對文章中詳述其作用。

由於我們以下大部分的計算都是基於矩陣乘法規則，如果你已經把線性代數還給了老師，請參考一下這裏: 維基百科-矩陣乘法

1.縮放(Scale)

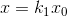
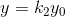
用矩陣表示:

$\left [ \begin{matrix} x\y\1\end{1} \right ] = \left [ \begin{matrix} k_1 & 0 & 0 \ 0 & k_2 & 0 \ 0 & 0 & 1\end{1} \right ] \left [ \begin{matrix} x_0 \y_0 \1\end{1} \right ]$

你可能注意到了，我們座標多了一個1，這是使用了齊次座標系的緣故，在數學中我們的點和向量都是這樣表示的(x, y)，兩者看起來一樣，計算機無法區分，爲此讓計算機也可以區分它們，增加了一個標誌位，增加之後看起來是這樣:

(x, y, 1) - 點
(x, y, 0) - 向量

另外，齊次座標具有等比的性質，(2,3,1)、(4,6,2)…(2N,3N,N)表示的均是(2,3)這一個點。(將MPERSP_2解釋爲scale這一誤解就源於此)。

圖例：

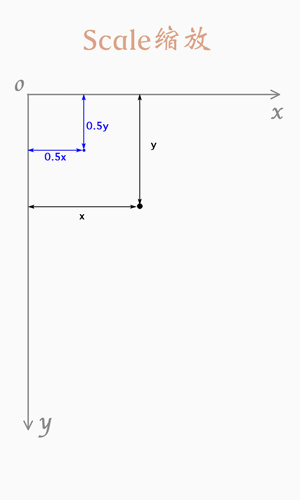
2.錯切(Skew)

錯切存在兩種特殊錯切，水平錯切(平行X軸)和垂直錯切(平行Y軸)。

水平錯切

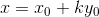
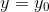
用矩陣表示:

$\left [ \begin{matrix} x\y\1\end{1} \right ] = \left [ \begin{matrix} 1 & k & 0 \ 0 & 1 & 0 \ 0 & 0 & 1\end{1} \right ] \left [ \begin{matrix} x_0\y_0\1\end{1} \right ]$

圖例:

垂直錯切

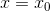
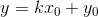
用矩陣表示:

$\left [ \begin{matrix} x\y\1\end{1} \right ] = \left [ \begin{matrix} 1 & 0 & 0 \ k & 1 & 0 \ 0 & 0 & 1\end{1} \right ] \left [ \begin{matrix} x_0\y_0\1\end{1} \right ]$

圖例:

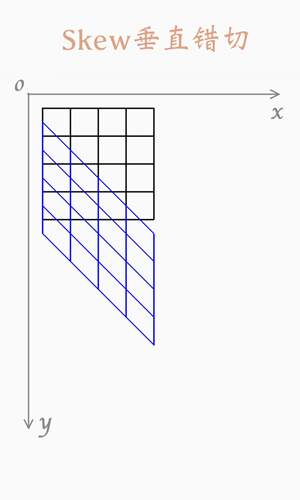
複合錯切

水平錯切和垂直錯切的複合。

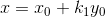
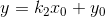
用矩陣表示:

$\left [ \begin{matrix} x\y\1\end{1} \right ] = \left [ \begin{matrix} 1 & k_1 & 0 \ k_2 & 1 & 0 \ 0 & 0 & 1\end{1} \right ] \left [ \begin{matrix} x_0\y_0\1\end{1} \right ]$

圖例:

3.旋轉(Rotate)

假定一個點 A(x0, y0) ,距離原點距離爲 r, 與水平軸夾角爲 α 度, 繞原點旋轉 θ 度, 旋轉後爲點 B(x, y) 如下:

$x_0 = r \cdot cos \alpha$

$y_0 = r \cdot sin \alpha$

$x = r \cdot cos( \alpha + \theta) = r \cdot cos \alpha \cdot cos \theta - r \cdot sin \alpha \cdot sin \theta = x_0 \cdot cos \theta - y_0 \cdot sin \theta$

$y = r \cdot sin( \alpha + \theta) = r \cdot sin \alpha \cdot cos \theta + r \cdot cos \alpha \cdot sin \theta = y_0 \cdot cos \theta + x_0 \cdot sin \theta$

用矩陣表示:

$\left [ \begin{matrix} x\y\1\end{1} \right ] = \left [ \begin{matrix} cos(\theta) & -sin(\theta) & 0 \sin(\theta) & cos(\theta) & 0 \0 & 0 & 1\end{1} \right ] . \left [ \begin{matrix} x_0\y_0\1\end{1} \right ]$

圖例:

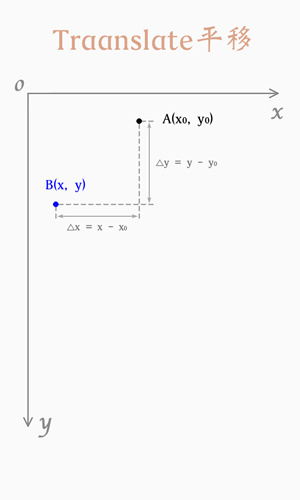
4.平移(Translate)

此處也是使用齊次座標的優點體現之一，實際上前面的三個操作使用 2x2 的矩陣也能滿足需求，但是使用 2x2 的矩陣，無法將平移操作加入其中，而將座標擴充套件爲齊次座標後，將矩陣擴充套件爲 3x3 就可以將演算法統一，四種演算法均可以使用矩陣乘法完成。

$x = x_0 + \Delta x$

$y = y_0 + \Delta y$

用矩陣表示:

$\left [ \begin{matrix} x\y\1\end{1} \right ] = \left [ \begin{matrix} 1 & 0 & \Delta x \0 & 1 & \Delta y \0 & 0 & 1\end{1} \right ] . \left [ \begin{matrix} x_0\y_0\1\end{1} \right ]$

圖例:

Matrix複合原理

其實Matrix的多種複合操作都是使用矩陣乘法實現的，從原理上理解很簡單，但是，使用矩陣乘法也有其弱點，後面的操作可能會影響到前面到操作，所以在構造Matrix時順序很重要。

我們常用的四大變換操作，每一種操作在Matrix均有三類,前乘(pre)，後乘(post)和設定(set)，可以參見文末對Matrix方法表，由於矩陣乘法不滿足交換律，所以前乘(pre)，後乘(post)和設定(set)的區別還是很大的。

前乘(pre)

前乘相當於矩陣的右乘：

$M' = M \cdot S$

這表示一個矩陣與一個特殊矩陣前乘後構造出結果矩陣。

後乘(post)

後乘相當於矩陣的左乘：

$M' = S \cdot M$

這表示一個矩陣與一個特殊矩陣後乘後構造出結果矩陣。

設定(set)

設定使用的不是矩陣乘法，而是直接覆蓋掉原來的數值，所以，使用設定可能會導致之前的操作失效。

組合

關於 Matrix 的文章終有一個問題，就是 pre 和 post 這一部分的理論非常彆扭，國內大多數文章都是這樣的，看起來貌似是對的但很難理解，部分內容違背直覺。

我由於也受到了這些文章的影響，自然而然的繼承了這一理論，直到在評論區有一位小夥伴提出了一個問題，才讓我重新審視了這一部分的內容，並進行了一定反思。

經過良久的思考之後，我決定拋棄國內大部分文章的那套理論和結論，只用嚴謹的數學邏輯和程式邏輯來闡述這一部分的理論，也許仍有疏漏，如有發現請指正。

首先澄清兩個錯誤結論，記住，是錯誤結論，錯誤結論，錯誤結論。

錯誤結論一：pre 是順序執行，post 是逆序執行。

這個結論很具有迷惑性，因爲這個結論並非是完全錯誤的，你很容易就能證明這個結論，例如下面下麪這樣：

// 第一段 pre  順序執行，先平移(T)後旋轉(R)
Matrix matrix = new Matrix();
matrix.preTranslate(pivotX,pivotY);
matrix.preRotate(angle);
Log.e("Matrix", matrix.toShortString());

// 第二段 post 逆序執行，先平移(T)後旋轉(R)
Matrix matrix = new Matrix();
matrix.postRotate(angle);
matrix.postTranslate(pivotX,pivotY)
Log.e("Matrix", matrix.toShortString());

這兩段程式碼最終結果是等價的，於是輕鬆證得這個結論的正確性，但事實真是這樣麼？

首先，從數學角度分析，pre 和 post 就是右乘或者左乘的區別，其次，它們不可能實際影響運算順序(程式執行順序)。以上這兩段程式碼等價也僅僅是因爲最終化簡公式一樣而已。

設原始矩陣爲 M，平移爲 T ，旋轉爲 R ，單位矩陣爲 I ，最終結果爲 M’

矩陣乘法不滿足交換律，即 AB ≠ BA

矩陣乘法滿足結合律，即 (AB)C = A(BC)

矩陣與單位矩陣相乘結果不變，即 A * I = A

由於上面例子中原始矩陣(M)是一個單位矩陣(I)，所以可得：

// 第一段 pre
M' = (M*T)*R = I*T*R = T*R

// 第二段 post
M' = T*(R*M) = T*R*I = T*R

由於兩者最終的化簡公式是相同的，所以兩者是等價的，但是，這結論不具備普適性。

即原始矩陣不爲單位矩陣的時候，兩者無法化簡爲相同的公式，結果自然也會不同。另外，執行順序就是程式書寫順序，不存在所謂的正序逆序。

錯誤結論二：pre 是先執行，而 post 是後執行。

這一條結論比上一條更離譜。

之所以產生這個錯誤完全是因爲寫文章的人懂英語。

pre  ：先，和 before 相似。
post ：後，和 after  相似。

所以就得出了 pre 先執行，而 post 後執行這一說法，但從嚴謹的數學和程式角度來分析，完全是不可能的，還是上面所說的，pre 和 post 不能影響程式執行順序，而程式每執行一條語句都會得出一個確定的結果，所以，它根本不能控制先後先後執行，屬於完全扯淡型。

如果非要用這套理論強行解釋的話，反而看起來像是 post 先執行，例如：

matrix.preRotate(angle);
matrix.postTranslate(pivotX,pivotY);

同樣化簡公式：

// 矩陣乘法滿足結合律
M‘ = T*(M*R) = T*M*R = (T*M)*R

從實際上來說，由於矩陣乘法滿足結合律，所以不論你說是靠右先執行還是靠左先執行，從結果上來說都沒有錯。

之前基於這條錯誤的結論我進行了一次錯誤的證明：

(這段內容註定要成爲我寫作歷程中不可抹滅的恥辱，既然是公開文章，就應該對讀者負責，雖然我在發表每一篇文章之前都竭力的求證其中的問題，各種細節，避免出現這種錯誤，但終究還是留下了這樣一段內容，在此我誠摯的向我所有的讀者道歉。)

關注我的讀者請儘量看我在個人部落格和 GitHub 發佈的版本，這兩個平臺都在博文修復計劃之內，有任何錯誤或者紕漏，都會首先修復這兩個平臺的文章。另外，所有進行修復過的文章都會在我的微博 @GcsSloop 重新發布說明，關注我的微博可以第一時間得到博文更新或者修復的訊息。

以下是錯誤證明：

在實際操作中，我們每一步操作都會得出準確的計算結果，但是爲什麼還會用存在先後先後的說法? 難道真的能夠用pre和post影響計算順序? 實則不然，下面下麪我們用一個例子說明:~~
Matrix matrix = new Matrix();
matrix.postScale(0.5f, 0.8f);
matrix.preTranslate(1000, 1000);
Log.e(TAG, "MatrixTest" + matrix.toShortString());
在上面的操作中，如果按照正常的思路，先縮放，後平移，縮放操作執行在前，不會影響到後續的平移操作，但是執行結果卻發現平移距離變成了(500， 800)。~~

在上面例子中，計算順序是沒有問題的，先計算的縮放，然後計算的平移，而縮放影響到平移則是因爲前一步縮放後的結果矩陣右乘了平移矩陣，這是符合矩陣乘法的運算規律的，也就是說縮放操作雖然在前卻影響到了平移操作，相當於先執行了平移操作，然後執行的縮放操作，因此纔有pre操作會先執行，而post操作會後執行這一說法。~~

上面的論證是完全錯誤的，因爲可以輕鬆舉出反例：
Matrix matrix = new Matrix();
matrix.preScale(0.5f, 0.8f);
matrix.preTranslate(1000, 1000);
Log.e(TAG, "MatrixTest" + matrix.toShortString());
反例中，雖然將 postScale 改爲了 preScale ，但兩者結果是完全相同的，所以先後先後論根本就是錯誤的。

他們結果相同是因爲最終化簡公式是相同的，都是 S*T

之所以平移距離是 MTRANS_X = 500，MTRANS_Y = 800，那是因爲執行 Translate 之前 Matrix 已經具有了一個縮放比例。在右乘的時候影響到了具體的數值計算，可以用矩陣乘法計算一下。

$\left [ \begin{matrix} 0.5 & 0 & 0 \0 & 0.8 & 0 \0 & 0 & 1\end{1} \right ] \cdot \left [ \begin{matrix} 1 & 0 & 1000 \0 & 1 & 1000 \0 & 0 & 1\end{1} \right ] = \left [ \begin{matrix} 0.5*1+0*0+0*0 & 0.5*0+0*1+0*0 & 0.5*1000+0*1000+0*1\0*1+0.8*0+0*0 & 0*0+0.8*1+0*1 & 0*1000+0.8*1000+0*1\0*1+0*0+1*0 & 0*0+0*1+1*0 & 0*1000+0*1000+1*1\end{1} \right ]$

最終結果爲：

$\left [ \begin{matrix} 0.5 & 0 & 500\0 & 0.8 & 800\0 & 0 & 1\end{1} \right ]$

當 T*S 的時候，縮放比例則不會影響到 MTRANS_X 和 MTRANS_Y ，具體可以使用矩陣乘法自己計算一遍。

如何理解和使用 pre 和 post ？

不要去管什麼先後先後論，順序論，就按照最基本的矩陣乘法理解。

pre  : 右乘， M‘ = M*A
post : 左乘， M’ = A*M

那麼如何使用？

正確使用方式就是先構造正常的 Matrix 乘法順序，之後根據情況使用 pre 和 post 來把這個順序實現。

還是用一個最簡單的例子理解，假設需要圍繞某一點旋轉。

可以用這個方法 xxxRotate(angle, pivotX, pivotY) ,由於我們這裏需要組合構造一個 Matrix，所以不直接使用這個方法。

首先，有兩條基本定理：

所有的操作(旋轉、平移、縮放、錯切)預設都是以座標原點爲基準點的。
之前操作的座標系狀態會保留，並且影響到後續狀態。

基於這兩條基本定理，我們可以推算出要基於某一個點進行旋轉需要如下步驟：

1. 先將座標系原點移動到指定位置，使用平移 T
2. 對座標系進行旋轉，使用旋轉 S (圍繞原點旋轉)
3. 再將座標系平移回原來位置，使用平移 -T

具體公式如下：

M 爲原始矩陣，是一個單位矩陣， M‘ 爲結果矩陣， T 爲平移， R爲旋轉

M' = M*T*R*-T = T*R*-T

按照公式寫出來的虛擬碼如下：

Matrix matrix = new Matrix();
matrix.preTranslate(pivotX,pivotY);
matrix.preRotate(angle);
matrix.preTranslate(-pivotX, -pivotY);

圍繞某一點操作可以拓展爲通用情況，即：

Matrix matrix = new Matrix();
matrix.preTranslate(pivotX,pivotY);
// 各種操作，旋轉，縮放，錯切等，可以執行多次。
matrix.preTranslate(-pivotX, -pivotY);

公式爲：

M' = M*T* ... *-T = T* ... *-T

但是這種方式，兩個調整中心的平移函數就拉的太開了，所以通常採用這種寫法：

Matrix matrix = new Matrix();
// 各種操作，旋轉，縮放，錯切等，可以執行多次。
matrix.postTranslate(pivotX,pivotY);
matrix.preTranslate(-pivotX, -pivotY);

這樣公式爲：

M' = T*M* ... *-T = T* ... *-T

可以看到最終化簡結果是相同的。

所以說，pre 和 post 就是用來調整乘法順序的，正常情況下應當正向進行構建出乘法順序公式，之後根據實際情況調整書寫即可。

在構造 Matrix 時，個人建議儘量使用一種乘法，前乘或者後乘，這樣操作順序容易確定，出現問題也比較容易排查。當然，由於矩陣乘法不滿足交換律，前乘和後乘的結果是不同的，使用時應結合具體情景分析使用。

下面下麪我們用不同對方式來構造一個相同的矩陣:

注意:

1.由於矩陣乘法不滿足交換律，請保證使用初始矩陣(Initial Matrix)，否則可能導致運算結果不同。
2.注意構造順序，順序是會影響結果的。
3.Initial Matrix是指new出來的新矩陣，或者reset後的矩陣，是一個單位矩陣。

1.僅用pre：

// 使用pre， M' = M*T*S = T*S
Matrix m ＝ new Matrix();
m.reset();
m.preTranslate(tx, ty); 
m.preScale(sx, sy);

用矩陣表示:

$\left [ \begin{matrix} & &\ & Result Matrix &\ & &\end{1} \right ] = \left [ \begin{matrix} & &\ & Initial Matrix &\ & &\end{1} \right ] \cdot \left [ \begin{matrix} 1 & 0 & \Delta x \0 & 1 & \Delta y \0 & 0 & 1\end{1} \right ] \cdot \left [ \begin{matrix} sx & 0 & 0\0 & sy & 0\0 & 0 & 1\end{1} \right ]$

2.僅用post:

// 使用post， M‘ = T*S*M = T*S
Matrix m ＝ new Matrix();
m.reset();
m.postScale(sx, sy);  //，越靠前越先執行。
m.postTranslate(tx, ty);

用矩陣表示:

$\left [ \begin{matrix} & &\ & Result Matrix &\ & &\end{1} \right ] = \left [ \begin{matrix} 1 & 0 & \Delta x \0 & 1 & \Delta y \0 & 0 & 1\end{1} \right ] \cdot \left [ \begin{matrix} sx & 0 & 0\0 & sy & 0\0 & 0 & 1\end{1} \right ]\cdot \left [ \begin{matrix} & &\ & Initial Matrix &\ & &\end{1} \right ]$

3.混合:

// 混合 M‘ = T*M*S = T*S
Matrix m ＝ new Matrix();
m.reset();
m.preScale(sx, sy);  
m.postTranslate(tx, ty);

或:

// 混合 M‘ = T*M*S = T*S
Matrix m ＝ new Matrix();
m.reset();
m.postTranslate(tx, ty);
m.preScale(sx, sy);

由於此處只有兩步操作，且指定了先後先後，所以程式碼上交換並不會影響結果。

用矩陣表示:

$\left [ \begin{matrix} & &\ & Result Matrix &\ & &\end{1} \right ] = \left [ \begin{matrix} 1 & 0 & \Delta x \0 & 1 & \Delta y \0 & 0 & 1\end{1} \right ] \cdot \left [ \begin{matrix} & &\ & Initial Matrix &\ & &\end{1} \right ] \cdot \left [ \begin{matrix} sx & 0 & 0\0 & sy & 0\0 & 0 & 1\end{1} \right ]$

注意: 由於矩陣乘法不滿足交換律，請保證初始矩陣爲單位矩陣，如果初始矩陣不爲單位矩陣，則導致運算結果不同。

上面雖然用了很多不同的寫法，但最終的化簡公式是一樣的，這些不同的寫法，都是根據同一個公式反向推算出來的。

Matrix方法表

這個方法表，暫時放到這裏讓大家看看，方法的使用講解放在下一篇文章中。

方法類別	相關API	摘要
基本方法	equals hashCode toString toShortString	比較、獲取雜湊值、轉換爲字串
數值操作	set reset setValues getValues	設定、重置、設定數值、獲取數值
數值計算	mapPoints mapRadius mapRect mapVectors	計算變換後的數值
設定(set)	setConcat setRotate setScale setSkew setTranslate	設定變換
前乘(pre)	preConcat preRotate preScale preSkew preTranslate	前乘變換
後乘(post)	postConcat postRotate postScale postSkew postTranslate	後乘變換
特殊方法	setPolyToPoly setRectToRect rectStaysRect setSinCos	一些特殊操作
矩陣相關	invert isAffine isIdentity	求逆矩陣、是否爲仿射矩陣、是否爲單位矩陣 …

總結

對於Matrix重在理解，理解了其中的原理之後用起來將會更加得心應手。

續集：

粉絲技術交流扣裙
在这里插入图片描述

Android自定義控制元件進階09-控制元件核心Matrix原理

⚠️ 警告：測試本文章範例之前請關閉硬體加速。

Matrix簡介

Matrix特點

常見誤解

Matrix基本原理

1.縮放(Scale)

2.錯切(Skew)

水平錯切

垂直錯切

複合錯切

3.旋轉(Rotate)

4.平移(Translate)

Matrix複合原理

前乘(pre)

後乘(post)

設定(set)

組合

錯誤結論一：pre 是順序執行，post 是逆序執行。

錯誤結論二：pre 是先執行，而 post 是後執行。

以下是錯誤證明：

如何理解和使用 pre 和 post ？

下面 下麪我們用不同對方式來構造一個相同的矩陣:

1.僅用pre：

2.僅用post:

3.混合:

Matrix方法表

總結

續集：

下面下麪我們用不同對方式來構造一個相同的矩陣: