寫在前面：博主是一位普普通通的19屆二本大學生，平時最大的愛好就是聽聽歌，逛逛B站。博主很喜歡的一句話花開堪折直須折，莫待無花空折枝：博主的理解是頭一次爲人，就應該做自己想做的事，做自己不後悔的事，做自己以後不會留有遺憾的事，做自己覺得有意義的事，不浪費這大好的青春年華。博主寫部落格目的是記錄所學到的知識並方便自己複習，在記錄知識的同時獲得部分瀏覽量，得到更多人的認可，滿足小小的成就感，同時在寫部落格的途中結交更多志同道合的朋友，讓自己在技術的路上並不孤單。

目錄:
1.最小生成樹
        生成樹概念
        最小生成樹
2.普裡姆演算法【Prim】
        普裡姆演算法簡介
        普裡姆演算法完整程式碼實現 (C語言)
        普裡姆演算法小結
3.克魯斯卡爾演算法【Kruskal】
        克魯斯卡爾演算法簡介
        克魯斯卡爾演算法完整程式碼實現 (C語言)
        克魯斯卡爾演算法小結

1.最小生成樹

1.1生成樹概念

對連通圖進行遍歷，過程中所經過的邊和頂點的組合可看做是一棵普通樹，通常稱爲生成樹。生成樹也理解爲包含所有頂點的極小連通子圖（極小連通子圖後邊會講）

連通圖中的生成樹必須滿足以下 2 個條件：
1.包含連通圖中所有的頂點；
2.任意兩頂點之間有且僅有一條通路；
因此，連通圖的生成樹具有這樣的特徵，即生成樹中邊的數量 = 頂點數 - 1。

1.2最小生成樹

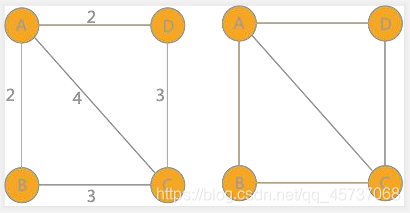
對於含有 n 個頂點的連通圖來說可能包含有多種生成樹，例如圖 1 所示：

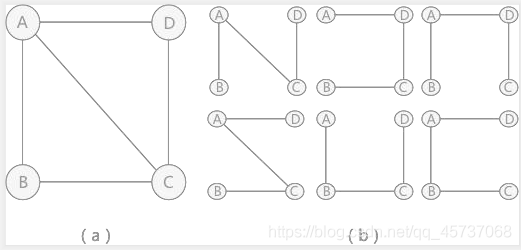
上圖中的連通圖和它相對應的生成樹，可以用於解決實際生活中的問題：假設 A、B、C 和 D 爲 4 座城市，爲了方便生產生 活，要爲這 4 座城市建立通訊。對於 4 個城市來講，本着節約經費的原則，只需要建立 3 個通訊線路即可，就如圖 1（b） 中的任意一種方式。 在具體選擇採用（b）中哪一種方式時，需要綜合考慮城市之間間隔的距離，建設通訊線路的難度等各種因素，將這些因素綜合 起來用一個數值表示，當作這條線路的權值。

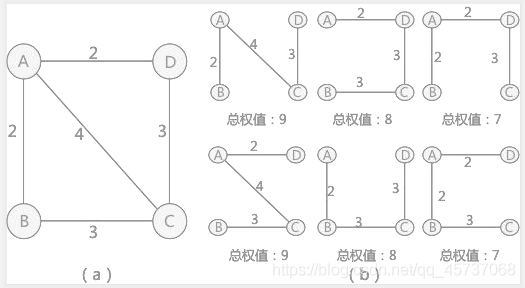
假設通過綜合分析，城市之間的權值如圖 2（a）所示，對於（b）的方案中，選擇權值總和爲 7 的兩種方案最節約經費。 這就是本節要討論的最小生成樹的問題，簡單得理解就是給定一個帶有權值的連通圖（連通網），如何從衆多的生成樹中篩選出 權值總和最小的生成樹，即爲該圖的 最小生成樹

給定一個連通網，求最小生成樹的方法有：普裡姆（Prim）演算法和克魯斯卡爾（Kruskal）演算法。

2.普裡姆演算法【Prim】

2.1普裡姆演算法簡介

普裡姆演算法在找最小生成樹時，將頂點分爲兩類:一類是在查詢的過程中已經包含在樹中的（假設爲 A 類），剩下的是另一類 （假設爲 B 類）。
對於給定的連通網，起始狀態全部頂點都歸爲 B 類。在找最小生成樹時，選定任意一個頂點作爲起始點，並將之從 B 類移至 A
類；然後找出 B 類中到 A 類中的頂點之間權值最小的頂點，將之從 B 類移至 A 類，如此重複，直到 B 類中沒有頂點爲止。 所走過的頂點和邊就是該連通圖的最小生成樹。

例如，通過普裡姆演算法查詢上圖的最小生成樹的步驟爲： 假如從頂點 A 出發，頂點 B、C、D 到頂點 A 的權值分別爲 2、4、2，所以，對於頂點 A 來說，頂點 B 和頂點 D 到 A 的 權值最小，假設先找到的頂點 B：

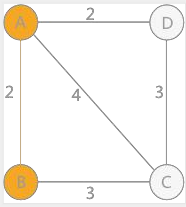
繼續分析頂點 C 和 D，頂點 C 到 B 的權值爲 3，到 A 的權值爲 4；頂點 D 到 A 的權值爲 2，到 B 的權值爲無窮大（如 果之間沒有直接通路，設定權值爲無窮大）。所以頂點 D 到 A 的權值最小：

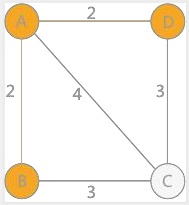
最後，只剩下頂點 C，到 A 的權值爲 4，到 B 的權值和到 D 的權值一樣大，爲 3。所以該連通圖有兩個最小生成樹：

2.2普裡姆演算法完整程式碼實現 (C語言)

#include <stdio.h>
#include <stdlib.h>
#define VertexType int
#define VRType int
#define MAX_VERtEX_NUM 20
#define InfoType char #define INFINITY 65535
typedef struct {
    VRType adj; //對於無權圖，用 1 或 0 表示是否相鄰；對於帶權圖，直接爲權值。
    InfoType * info; //弧額外含有的資訊指針
}ArcCell,AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];
typedef struct {
    VertexType vexs[MAX_VERtEX_NUM]; //儲存圖中頂點數據
    AdjMatrix arcs; //二維陣列，記錄頂點之間的關係
    int vexnum,arcnum; //記錄圖的頂點數和弧（邊）數
}MGraph;
//根據頂點本身數據，判斷出頂點在二維陣列中的位置
int LocateVex(MGraph G,VertexType v){
    int i=0;
    //遍歷一維陣列，找到變數 v
    for (; i<G.vexnum; i++) {
    if (G.vexs[i]==v) {
     return i;
    }
  }
    return -1;
}
//構造無向網
void CreateUDN(MGraph* G){
   scanf("%d,%d",&(G->vexnum),&(G->arcnum));
   for (int i=0; i<G->vexnum; i++) {
    scanf("%d",&(G->vexs[i]));
  }
  for (int i=0; i<G->vexnum; i++) {
   for (int j=0; j<G->vexnum; j++) {
     G->arcs[i][j].adj=INFINITY;
     G->arcs[i][j].info=NULL;
    }
  }
  for (int i=0; i<G->arcnum; i++) {
     int v1,v2,w; scanf("%d,%d,%d",&v1,&v2,&w);
     int m=LocateVex(*G, v1);
     int n=LocateVex(*G, v2);
     if (m==-1 ||n==-1) {
     printf("no this vertex\n");
     return;
    }
    G->arcs[n][m].adj=w;
    G->arcs[m][n].adj=w;
  }
}
//輔助陣列，用於每次篩選出權值最小的邊的鄰接點
typedef struct {
   VertexType adjvex;//記錄權值最小的邊的起始點
   VRType lowcost;//記錄該邊的權值
}closedge[MAX_VERtEX_NUM]; closedge theclose;//建立一個全域性陣列，因爲每個函數中都會使用到
//在輔助陣列中找出權值最小的邊的陣列下標，就可以間接找到此邊的終點頂點。
int minimun(MGraph G,closedge close){
   int min=INFINITY;
   int min_i=-1;
   for (int i=0; i<G.vexnum; i++) {
//權值爲 0，說明頂點已經歸入最小生成樹中；然後每次和 min 變數進行比較，最後找出最小的。
   if (close[i].lowcost>0 && close[i].lowcost < min) { 
     min=close[i].lowcost; min_i=i;
   }
 }
  //返回最小權值所在的陣列下標
  return min_i;
}
//普裡姆演算法函數，G 爲無向網，u 爲在網中選擇的任意頂點作爲起始點
void miniSpanTreePrim(MGraph G,VertexType u){
//找到該起始點在頂點陣列中的位置下標
   int k=LocateVex(G, u);
   //首先將與該起始點相關的所有邊的資訊：邊的起始點和權值，存入輔助陣列中相應的位置，例如（1，2）邊，adjvex 爲 0， lowcost 爲 6，存入 theclose[1]中，輔助陣列的下標表示該邊的頂點 2
   for (int i=0; i<G.vexnum; i++) {
   if (i !=k) {
   theclose[i].adjvex=k;
   theclose[i].lowcost=G.arcs[k][i].adj;
    }
 }
//由於起始點已經歸爲最小生成樹，所以輔助陣列對應位置的權值爲 0，這樣，遍歷時就不會被選中
  theclose[k].lowcost=0;
//選擇下一個點，並更新輔助陣列中的資訊
  for (int i=1; i<G.vexnum; i++) {
//找出權值最小的邊所在陣列下標
   k=minimun(G, theclose);
//輸出選擇的路徑
   printf("v%d v%d\n",G.vexs[theclose[k].adjvex],G.vexs[k]);
//歸入最小生成樹的頂點的輔助陣列中的權值設爲 0
   theclose[k].lowcost=0;
//資訊輔助陣列中儲存的資訊，由於此時樹中新加入了一個頂點，需要判斷，由此頂點出發，到達其它各頂點的權值是否比之前記錄的權值還要小，如果還小，則更新
  for (int j=0; j<G.vexnum; j++) {
   if (G.arcs[k][j].adj<theclose[j].lowcost) {
    theclose[j].adjvex=k;
    theclose[j].lowcost=G.arcs[k][j].adj;
   }
  }
 }
   printf("\n");
}
int main(){
   MGraph G;
   CreateUDN(&G); miniSpanTreePrim(G, 1);
}

2.3普裡姆演算法小結

普裡姆演算法的執行效率只與連通網中包含的頂點數相關，而和網所含的邊數無關。所以普裡姆演算法適合於解決邊稠密的網，該演算法執行的時間複雜度爲：O(n²)
如果連通網中所含邊的綢密度不高，則建議使用克魯斯卡爾演算法求最小生成樹（下面 下麪會講）。

3.克魯斯卡爾演算法

3.1克魯斯卡爾演算法簡介

對於任意一個連通網的最小生成樹來說，在要求總的權值最小的情況下，最直接的想法就是將連通網中的所有邊按照權值大小進行升序排序，從小到大依次選擇。

由於最小生成樹本身是一棵生成樹，所以需要時刻滿足以下兩點：

• 生成樹中任意頂點之間有且僅有一條通路，也就是說，生成樹中不能存在迴路；
• 對於具有 n 個頂點的連通網，其生成樹中只能有 n-1 條邊，這 n-1

所以克魯斯卡爾演算法的具體思路是：將所有邊按照權值的大小進行升序排序，然後從小到大一一判斷，條件爲：如果這個邊不會與之前選擇的所有邊組成迴路，就可以作爲最小生成樹的一部分；反之，捨去。直到具有 n 個頂點的連通網篩選出來 n-1 條邊爲止。篩選出來的邊和所有的頂點構成此連通網的最小生成樹。

判斷是否會產生迴路的方法爲：在初始狀態下給每個頂點賦予不同的標記，對於遍歷過程的每條邊，其都有兩個頂點，判斷這兩個頂點的標記是否一致，如果一致，說明它們本身就處在一棵樹中，如果繼續連線就會產生迴路；如果不一致，說明它們之間還沒有任何關係，可以連線。假設遍歷到一條由頂點 A 和 B 構成的邊，而頂點 A 和頂點 B 標記不同，此時不僅需要將頂點 A 的標記更新爲頂點 B 的標記，還需要更改所有和頂點 A 標記相同的頂點的標記，全部改爲頂點 B 的標記。

如下例子，使用克魯斯卡爾演算法找最小生成樹的過程爲：：

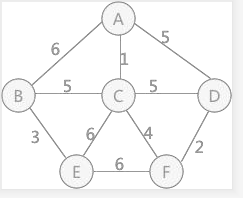
首先，在初始狀態下，對各頂點賦予不同的標記（用顏色區別），如下圖所示：

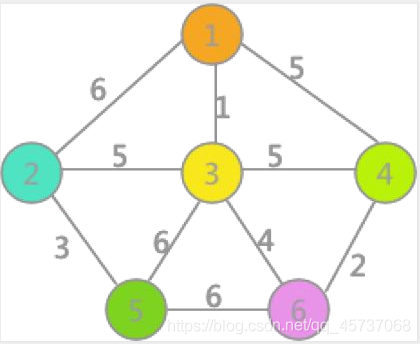
對所有邊按照權值的大小進行排序，按照從小到大的順序進行判斷，首先是（1，3），由於頂點 1 和頂點 3 標記不同，所以 可以構成生成樹的一部分，遍歷所有頂點，將與頂點 3 標記相同的全部更改爲頂點 1 的標記，如下：

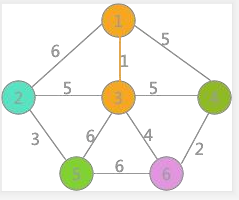
其次是（4，6）邊，兩頂點標記不同，所以可以構成生成樹的一部分，更新所有頂點的標記爲：

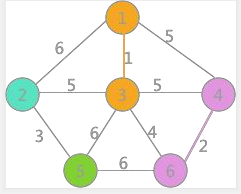
其次是（2，5）邊，兩頂點標記不同，可以構成生成樹的一部分，更新所有頂點的標記爲：

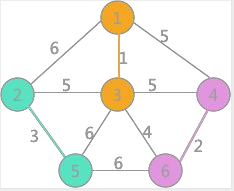
然後最小的是（3，6）邊，兩者標記不同，可以連線，遍歷所有頂點，將與頂點 6 標記相同的所有頂點的標記更改爲頂點 1 的標記：

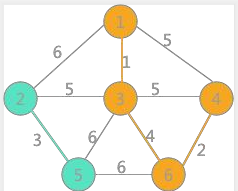
繼續選擇權值最小的邊，此時會發現，權值爲 5 的邊有 3 個，其中（1，4）和（3，4）各自兩頂點的標記一樣，如果連線會產生迴路，所以捨去，而（2，3）標記不一樣，可以選擇，將所有與頂點 2 標記相同的頂點的標記全部改爲同頂點 3 相同的標記：

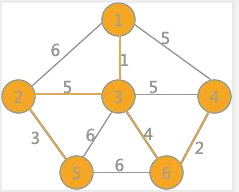
當選取的邊的數量相比與頂點的數量小 1 時，說明最小生成樹已經生成。所以最終採用克魯斯卡爾演算法得到的最小生成樹爲（6）所示

3.2克魯斯卡爾演算法完整程式碼實現 (C語言)

#include "stdio.h" 
#include "stdlib.h" 
#define MAX_VERtEX_NUM 20
#define VertexType int
typedef struct edge{
   VertexType initial;
   VertexType end;
   VertexType weight;
}edge[MAX_VERtEX_NUM];
//定義輔助陣列
typedef struct {
   VertexType value;//頂點數據
   int sign;//每個頂點所屬的集合
}assist[MAX_VERtEX_NUM]; assist assists;
//qsort 排序函數中使用，使 edges 結構體中的邊按照權值大小升序排序
int cmp(const void *a,const void*b){
  return ((struct edge*)a)->weight-((struct edge*)b)->weight;
}
//初始化連通網
void CreateUDN(edge *edges,int *vexnum,int *arcnum){
    printf("輸入連通網的邊數：\n");
    scanf("%d %d",&(*vexnum),&(*arcnum));
    printf("輸入連通網的頂點：\n");
    for (int i=0; i<(*vexnum); i++) {
     scanf("%d",&(assists[i].value)); assists[i].sign=i;
    }
    printf("輸入各邊的起始點和終點及權重：\n");
    for (int i=0 ; i<(*arcnum); i++) {
     scanf("%d,%d,%d",&(*edges)[i].initial,&(*edges)[i].end,&(*edges)[i].weight);
    }
}
//在 assists 陣列中找到頂點 point 對應的位置下標
int Locatevex(int vexnum,int point){
   for (int i=0; i<vexnum; i++) {
   if (assists[i].value==point) {
    return i;
   }
 }
  return -1;
}
int main(){
  int arcnum,vexnum; edge edges;
  CreateUDN(&edges,&vexnum,&arcnum);
//對連通網中的所有邊進行升序排序，結果仍儲存在 edges 陣列中
  qsort(edges, arcnum, sizeof(edges[0]), cmp);
//建立一個空的結構體陣列，用於存放最小生成樹
  edge minTree;
//設定一個用於記錄最小生成樹中邊的數量的常數
  int num=0;
//遍歷所有的邊
  for (int i=0; i<arcnum; i++) {
//找到邊的起始頂點和結束頂點在陣列 assists 中的位置
  int initial=Locatevex(vexnum, edges[i].initial);
  int end=Locatevex(vexnum, edges[i].end);
//如果頂點位置存在且頂點的標記不同，說明不在一個集閤中，不會產生迴路
  if (initial!=-1&& end!=-1&&assists[initial].sign!=assists[end].sign) {
//記錄該邊，作爲最小生成樹的組成部分
  minTree[num]=edges[i];
//計數+1 num++;
//將新加入生成樹的頂點標記全不更改爲一樣的
  for (int k=0; k<vexnum; k++) {
  if (assists[k].sign==assists[end].sign) {
   assists[k].sign=assists[initial].sign;
 }
}
//如果選擇的邊的數量和頂點數相差 1，證明最小生成樹已經形成，退出回圈
   if (num==vexnum-1) {
   break;  }
  }
 }
//輸出語句
  for (int i=0; i<vexnum-1; i++) {
  printf("%d,%d\n",minTree[i].initial,minTree[i].end);
 }
return 0;
}

3.3克魯斯卡爾演算法小結

剛剛介紹了求最小生成樹之普裡姆演算法。該演算法從頂點的角度爲出發點，時間複雜度爲 O(n2)，更適合與解決邊的綢密度更高 的連通網。 本節所介紹的克魯斯卡爾演算法，從邊的角度求網的最小生成樹，時間複雜度爲 O(eloge)。和普裡姆演算法恰恰相反，更適合於求 邊稀疏的網的最小生成樹