前言: $\quad$ 本文爲密碼學的數學基礎(王小雲版)讀書筆記,僅做了一些自認爲重要些的筆記,如有錯誤,歡迎指正.

同餘五大性質(重要)

a和b關於正整數m同餘等價於存在正整數k,使得$a-b=km$,記做:$a\equiv b (mod\ m)$,原書中同餘有七大性質,本文省去兩個,其他內容均以此五大性質爲基礎,因而需要深刻理解.

• 同餘式可以相加減, 即若有
  $\begin{array}{c} a \equiv b(\bmod m), \quad c \equiv d(\bmod m) \\則: a \pm c \equiv b \pm d(\bmod m) \end{array}$
• 同餘式可以相乘，即若
  $a \equiv b(\bmod m), \quad c \equiv d(\bmod m)$
  則有
  $a c \equiv b d(\bmod m)$
• (非常重要) $\quad$設 $d \geqslant 1, d \mid m,$ 若同餘式$a\equiv b (mod\ m)$ 成立, 則
  $a \equiv b(\bmod d)$
• 若 $m \geqslant 1,(a, m)=1,$ 則存在 $c$ 使得
  $c a \equiv 1(\bmod m)$
  我們把 c 稱爲 $a$ 對模 $m$ 的逆, 記作 $a^{-1}(\bmod m) .$
  可以根據歐幾裡得演算法得到.具體實現程式碼可見上一篇部落格.
• 同餘式組
  $a \equiv b\left(\bmod m_{j}\right), \quad j=1,2, \cdots, k$
  同時成立的充要條件是 $a \equiv b\left(\bmod \left[m_{1}, \cdots, m_{k}\right]\right)$
  公倍數一定是最小公倍數的乘積,加上性質3可以推出.

例2.5 設 n 爲整數, 試求出它能被 9 整除的充要條件.
解 $\quad$ 設 $n=a_{0} 10^{k}+\cdots+a_{k-1} 10+a_{k} . \quad$ 因爲 $10^{i} \equiv 1(\bmod 9), 1 \leqslant i \leqslant k,$ 所以
由同餘性質 1, 2 得
$n \equiv a_{0}+a_{1}+\cdots+a_{k}(\bmod 9)$
故
$9\left|a_{0}+a_{1}+\cdots+a_{k} \Leftrightarrow 9\right| n$
從例 2.5 同樣也可以推出 n 被 3 整除的充要條件爲 $3 \mid a_{0}+a_{1}+\cdots+a_{k},$ 這就 是我們早已熟知的判斷整數能否被 3 整除的方法.

(既約)剩餘類,(既約)剩餘系

(既約)剩餘類:
給定正整數m,所有對m同餘的陣列成的集合稱爲模m的一個剩餘類,以r表示m的一個剩餘類,如果$(r,m)=1$,則稱r爲模m的一個既約(或互素)剩餘類,模m的所有既約剩餘類的個數記作$\varphi (m)$,即爲我們常見的Euler函數
(既約)剩餘系:
關於m的所有(既約)剩餘類的集合稱爲模m的(既約)剩餘系.

• m個數完全剩餘系(通常稱爲剩餘系)的充要條件爲m個數兩兩對m不同餘
• $\varphi(m)$個數組成m的既約剩餘系的充要條件爲,$\varphi (m)$個數對m不同餘,且均與m互素.

構造方法(部分方法,有待補充)

定理 2.13 設 $m=m_{1} \cdots m_{k},$ 且 $m_{1}, \cdots, m_{k}$ 兩兩既約. 再設 $m=m_{j} M_{j}, 1 \leqslant j \leqslant k$, 及
$\begin{array}{l} \qquad x=M_{1} x^{(1)}+\cdots+M_{k} x^{(k)} \end{array}$
那麼 $x$ 遍歷模 $m$ 的完全（既約）剩餘系的充要條件是 $x^{(1)}, \cdots, x^{(k)}$ 分別遍歷 $m_{1}, \cdots, m_{k}$ 的完全 (既約) 剩餘系.
通常用於構造一個大數的(既約)剩餘系,可以根據此定理進行分解大數,然後進行一一組合,最終得到大數的(既約)剩餘系.爲方便程式設計與檢視結果,我利用$m=m_1m_2$,這一假設作爲前提,進行C語言程式碼實現,執行結果一覽: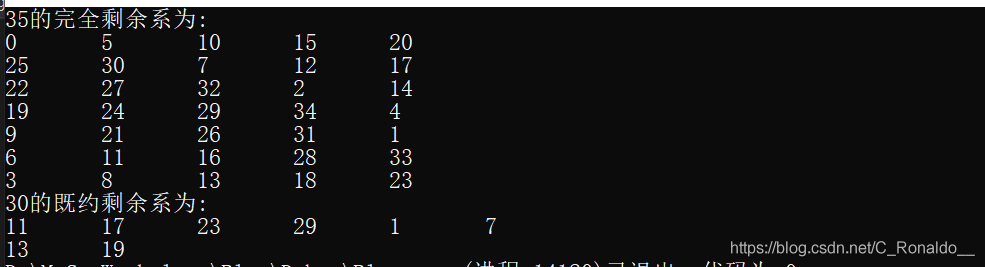
完整程式碼如下:

#include<iostream>
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b)
{
	if (!b)
		return a;
	return gcd(b, a % b);
}
ll* residual_system(ll m1, ll m2)//構造(完全)剩餘系
{
	if (gcd(m1, m2) != 1)
	{
		cout << "m1與m2不互素,輸入錯誤!" << endl;
		exit(-1);
	}
	ll M2 = m1, M1 = m2;
	ll* R = (ll*)malloc((m1 * m2+1) * sizeof(ll));//如果構造完全剩餘系,則共有m=m1*m2個元素
	if (!R)
		exit(-1);
	ll* Temp = R;
	ll x,x1=0,x2=0,m=m1*m2;
	for (x1 = 0; x1 < m1; ++x1)
	{
		for(x2 = 0; x2 < m2; ++x2)
		{
			x = (M1 * x1 + M2 * x2) % m;
			*Temp = x;
			Temp += 1;
			
		}
	}
	*Temp= -1;
	return R;

}
ll* Irreducible_residue_system(ll m1, ll m2)//構造既約剩餘系
{
	if (gcd(m1, m2) != 1)
	{
		cout << "m1與m2不互素,輸入錯誤!" << endl;
		exit(-1);
	}
	ll M2 = m1, M1 = m2;
	ll* R = (ll*)malloc((m1 * m2+1) * sizeof(ll));//如果構造既約剩餘系,則最多有m=m1*m2個元素
	if (!R)
		exit(-1);
	ll* Temp = R;
	ll x, x1 = 0, x2 = 0, m = m1 * m2;
	for (x1 = 0; x1 < m1; ++x1)
	{
		if (gcd(x1, m1) != 1)
			continue;
		for (x2 = 0; x2 < m2; ++x2)
		{
			if (gcd(x2 ,m2) != 1)
				continue;
			x = (M1 * x1 + M2 * x2) % m;
			*Temp = x;
			Temp += 1;

		}
	}
	*Temp = -1;//以-1作爲終止符號
	return R;
}
int main()
{
	ll m1 = 5, m2 = 7;
	ll* R = residual_system(m1, m2);
	cout <<m1 * m2<< "的完全剩餘係爲:" << endl;
	for (ll i = 0;R[i]!=-1; i++)
	{
		if (!(i % m1)&&i!=0)
			cout << '\n';
		cout << R[i] << '\t';
	}
	m1 = 6;
	m2 = 5;
	ll* R2 = Irreducible_residue_system(m1, m2);
	cout <<'\n'<<m1*m2<< "的既約剩餘係爲:" << endl;
	for (ll i = 0; R2[i] != -1; i++)
	{
		if (!(i % m1) && i != 0)
			cout << '\n';
		cout << R2[i] << '\t';
	}
	return 0;
}

Euler定理,Wilson定理

定理描述與證明

模 m 的既約剩餘系可以取種種不同的形式，但不難看出每個既約剩餘系中所 有數的乘積模 $m$ 是不變的, 即若 $\left\{r_{0}, \cdots, r_{\varphi(m)-1}\right\},\left\{r_{0}^{\prime}, \cdots, r_{\varphi(m)-1}^{\prime}\right\}$ 是模 $m$ 的兩
個既約剩餘系, 那麼必有
$\prod_{j=1}^{\varphi(m)} r_{j} \equiv \prod_{j=1}^{\varphi(m)} r_{j}^{\prime}(\bmod m)$
由此就可得到下面 下麪著名的Euler 定理.
Euler 定理 $\quad$ 設 $(a, m)=1,$ 則有
$a^{\varphi(m)} \equiv 1(\bmod m)$
證明 :$\quad$ 取 $r_{0}, \cdots, r_{\varphi(m)-1} \quad$ 是模 $m$ 的一組既約剩餘系，由定理 2.11 :
設 $a, b$ 是任意整數，且 $(a, m)=1,$ 那麼，x 遍歷模 $m$ 的一組 完全剩餘系時, ax + b 也遍歷模 m 的一組完全剩餘系。
知:
當 $(a, m)=1$ 時, $a r_{0}, \cdots, a r_{\varphi(m)-1}$ 也是模 $m$ 的既約剩餘系，同時
因此
$\prod_{j=0}^{\varphi(m)-1} r_{j} \equiv \prod_{j=0}^{\varphi(m)-1}\left(a r_{j}\right) \equiv a^{\varphi(m)} \prod_{j=0}^{\varphi(m)-1} r_{j}(\bmod m)$
由於 $\left(r_{j}, m\right)=1, j=0, \cdots, \varphi(m)-1,$ 所以
$a^{\varphi(m)} \equiv 1(\bmod m)$
Wilson 定理$\quad$設 $p$ 是素數, $r_{1}, \cdots, r_{p-1}$ 是模 $p$ 的既約剩餘系，則
$\prod_{r \bmod p} r \equiv r_{1} \cdots r_{p-1} \equiv-1(\bmod p)$
特別地有
$(p-1) ! \equiv-1(\bmod p)$
證明…有時間再補充,主要思路爲利用配對思想進行配對

Euler定理應用:

歐拉定理是費馬小定理的推廣和一般化,常見的應用如下:

1.RSA公鑰密碼體制

在計算機領域中廣泛使用的RSA公鑰密碼演算法也正是以歐拉函數爲基礎的。基於歐拉定理及大數的素因子分解極爲困難而提出的RSA公鑰密碼體制在1977年由羅納德·李維斯特、阿迪·薩莫爾和倫納德·阿德曼一起提出。RSA加密體制廣泛應用於資訊保安領域中的資訊加密和數位簽名,其應用原理是產生一對金鑰,一個爲使用者所保留,另一個則可以爲任意使用者獲得，並且很難通過一個金鑰去獲取另一個金鑰,從而保證公鑰體制的安全性。
（1）演算法簡介。設p，q爲兩個保密的充分大的質數，n=pq,則φ(n)=(p-1)(q-1)；取一個整數e，滿足1<e<φ(n),且滿足(e,φ(n))=1；求出e關於φ(n)的逆元d，使得$ed=1(mod\ \varphi (n))$；則可以（d，n）爲金鑰，以（e，n）爲公鑰，或者以（e，n）爲金鑰，以（d，n）爲公鑰.隨即銷燬p與q。
加解密的方法爲加密：$C=M^e（mod\ n）$其中M表示明文，C表示密文。解密：$M=C^d（mod\ n）$其中M表示明文，C表示密文。要證明這樣的加解密方式是可行的，只需證明：對任意整數k，有$k^{ed}=k(mod\ n)$這等價於$km\varphi (n)+1=k(mod\ n)$若(k,n)=1,則原式等價於$(k\varphi (n))m=1(mod\ n)$，顯然成立；若k=mp，原式等價於$(mp)^{α\varphi (n)+1}m=m(mod\ q)$,與前面相同；若k爲n倍數，則顯然成立。則證畢。通常用公鑰加密，金鑰解密。
（2）RSA的優缺點。RSA演算法是目前理論上最爲完善的公鑰密碼體制，是公鑰密碼體制中最優秀、影響最大的加密演算法。RSA的安全性是基於大整數素因子分解的困難性，在理論上一直未能得到證明。RSA經歷了各種攻擊，至今未能被完全攻破。但數學上至今未能證明分解就是攻擊RSA的最佳方法，不排除今後有發現多項式時間內分解的演算法。並且，囿於素數產生技術的限制，生產亂數的程式必須不能給攻擊者任何資訊，即保證隨機性與不可預測性，故生產金鑰的複雜度也較高。另外，由於進行的都是非常大的數的計算，RSA的速度不可避免地被拖慢，比對應同樣安全級別的對稱密碼演算法慢近1000倍。

2.羣論中的運用

在羣論中的運用有限回圈羣生成元個數的計算公式可以用歐拉函數表出。G爲回圈羣是指G的每個元都是G的某一固定的元a的乘方，即對於任何≤n且與n互素的正整數r,αr是G的生成元。若G是n階回圈羣,則G含有φ(n)個生成元。

Wilson定理應用:

Wilson定理的應用常用於計算化簡以及一些證明題中,見習題1第(2)問.

習題

題目描述

1. 設素數 p 爲奇數, 證明:

• [ 1 ] . 當 $p=4 m+3$ 時, 對任意整數 $a$ 均有 $a^{2} \not \equiv-1(\bmod p)$
• [ 2 ]. 當 $p=4 m+1$ 時, 必有整數 $a$ 滿足 $a^{2} \equiv-1(\bmod p) .$

2. 設 $m=m_{1} m_{2} \cdots m_{k}, m_{1}, m_{2}, \cdots, m_{k}$ 兩兩既約, $\left(m, a_{i}\right)=1$. 證明: $\stackrel{\text { 當 }}{=} x^{(i)}$ 分別遍
   歷 $m_{i}$ 的完全 (既約) 剩餘系時,
   $x=\left(M_{1} a_{1} x^{(1)}+M_{2}+\cdots+M_{k}\right)\left(M_{1}+M_{2} a_{2} x^{(2)}+\cdots+M_{k}\right) \cdots\left(M_{1}+M_{2}+\cdots+M_{k} a_{k} x^{(k)}\right)$
   $x=m_{1}^{1} a_{1} x^{11}+m_{2} a_{2} x^{12} \ldots n_{k}^{k} a_{n}$

參考思路

(1).反證法:假設成立,存在 $a$ 使 $a^{2} \equiv-1$ $(\bmod p),$ then $a^{p-1} \equiv a^{2(2 m+1)} \equiv(-1)^{2 m+1} \equiv-1(\bmod p),$ since $p \neq 2$ 這與歐拉定理矛盾,得證.
(2) Let $a=(2m) !,$ then
$\begin{aligned} a^{2} &=(1 \times 2 \times \cdots \times 2 m)(1 \times 2 \times \cdots \times 2 m) \\ & \equiv(1 \times 2 \times \cdots \times 2 m)[(-1)(p-1) \times(-1)(p-2) \times \cdots \times(-1)(2 m+1)] \quad(\bmod p) \\ & \equiv(-1)^{2 m}(p !) \quad(\bmod p) \\ & \equiv-1 \quad(\bmod p) \end{aligned}$(非常巧妙地運用了Wilson定理)
2.待補充…

參考論文:孫焱. 歐拉函數的性質及簡單應用[J]. 商情, 2017, 000(048):288.