Floyd演算法的原理和實現程式碼

原理

假設有向圖G=(V，E)採用鄰接矩陣儲存。設定一個二維陣列A用於存放當前頂點之間的最短路徑長度，分量A[i][j]表示當前頂點i -> j的最短路徑長度。然後，每次新增一個頂點，同時對A的陣列進行篩選優化，期間會產生k個A陣列。Ak[i][j]陣列代表着從考慮0 -> k的i -> j 的最小距離，當k 等於全部頂點數的時候，就是已經找出了i -> j 的最短距離。

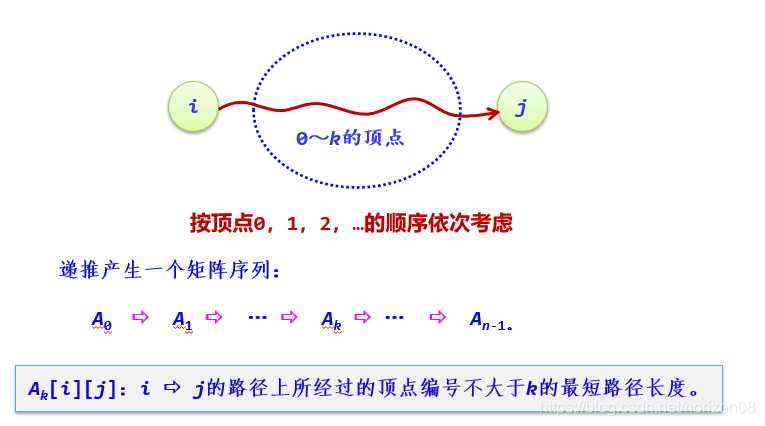
初始化

1. 二維陣列 path [i] [j] 初始化時，i -> j有路徑時，path [i] [j] = i (即指向j的前一個頂點位置); 沒有路徑時path [i] [j] 初始化爲-1。

2.二維陣列A[i][j] 初始化時就等價於邊 i -> j 的權值。

演算法過程

1. 用二維陣列A儲存最短路徑長度：

   • Ak[i][j]表示考慮頂點0~k後得出的i -> j的最短路徑長度。
   • An-1[i][j]表示最終的i -> j的最短路徑長度。

2. 用二維陣列path存放最短路徑：

   • pathk[i][j]表示考慮頂點0~k後得出的i -> j的最短路徑。
   • pathn-1[i][j]表示最終i -> j的最短路徑。

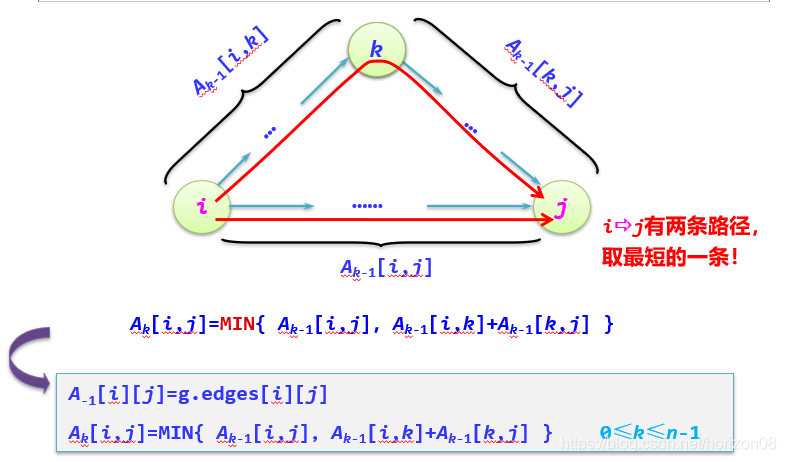
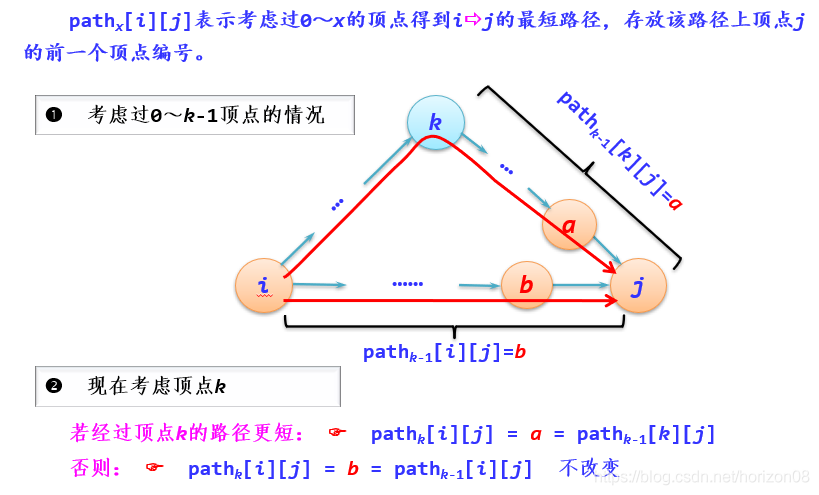
實際上就是從一個個頂點開始分析，從一個到多個的過程中去篩選。初始化數據後，開始新增節點1，再去分析如果包含了節點1以後的各點之間路徑是不是有變短，如果有的話就替換，這一遍分析過程被稱爲二維陣列A的更新，也就是Ak陣列，k是分析的節點1。而我們的path陣列則是用來存放路徑，其實就是i->j的路徑上的j的上一步的頂點。

3.路徑的求解

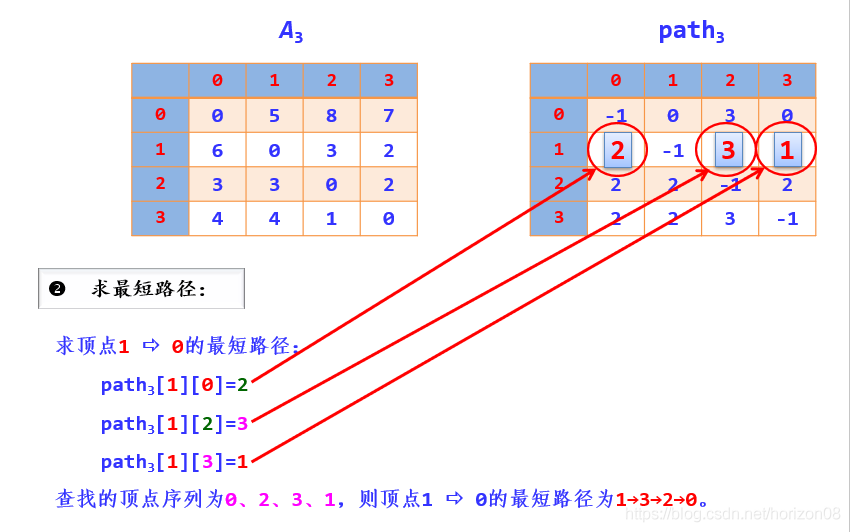
實現

Floyd演算法的C語言實現如下：

void Floyd(MatGraph g)	//求每對頂點之間的最短路徑
{  int A[MAXVEX][MAXVEX];	//建立A陣列
   int path[MAXVEX][MAXVEX];	//建立path陣列
　 int i, j, k;
　 for (i=0;i<g.n;i++)   		
     for (j=0;j<g.n;j++) 
     {  A[i][j]=g.edges[i][j];
        if (i!=j && g.edges[i][j]<INF)
	    path[i][j]=i; 	//i和j頂點之間有一條邊時
　　　　 else			//i和j頂點之間沒有一條邊時
	    path[i][j]=-1;
     }
     //以上是初始化過程內容
   for (k=0;k<g.n;k++)		//求Ak[i][j]
　 {   for (i=0;i<g.n;i++)
　　　    for (j=0;j<g.n;j++)
	　   if (A[i][j]>A[i][k]+A[k][j])	//找到更短路徑
	　   {　  A[i][j]=A[i][k]+A[k][j];	//修改路徑長度
	　        path[i][j]=path[k][j]; 	//修改最短路徑爲經過頂點k
　　　　    }
　 }
　     DispathFloyd(g, A, path);
}	

//以下爲輸出最短路徑的函數
void DispathFloyd(MatGraph g, int A[][MAXV], int path[][MAXV])
{
    int i, j, k, s;
    int apath[MAXV], d;

    for (i = 0; i < g.n; i++)
        for (j = 0; j < g.n; j++)
        {
            if (A[i][j] != INF && i != j)
            {
                printf("從%d到%d的路徑是：", i, j);
                k = path[i][j];
                d = 0;
                apath[d] = j;
                while (k != -1 && k != i)
                {
                    d++;
                    apath[d] = k;
                    k = path[i][k];
                }
                d++;
                apath[d] = i;
                printf("%d", apath[d]);

                for (s = d - 1; s >= 0; s--)
                    printf(",%d", apath[s]);
                printf("\t路徑長度爲:%d\n", A[i][j]);
            }
        }
}

可以看出時間複雜度爲O(n^3)

Enjoy