距離

在幾何學裡面距離並不單指直線距離，有很多其他的距離沒有那麼常用，但考場上可能會出現，為了防止題目不給出定義等，我們有必要認識一下各種距離。

~~後面的角標為了清楚直接打到字母后面了~~

歐幾里得距離

也被稱作歐式距離，在平面直角座標系中，設有兩點 \(A(x_{1},y_{1}),B(x_{2},y_{2})\)，他們的歐幾里得距離其實就是兩點所連成的線段的長度，初中也講過計算公式：

\[|AB|=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}} \]

這個公式怎麼來的呢？看一下這張圖：

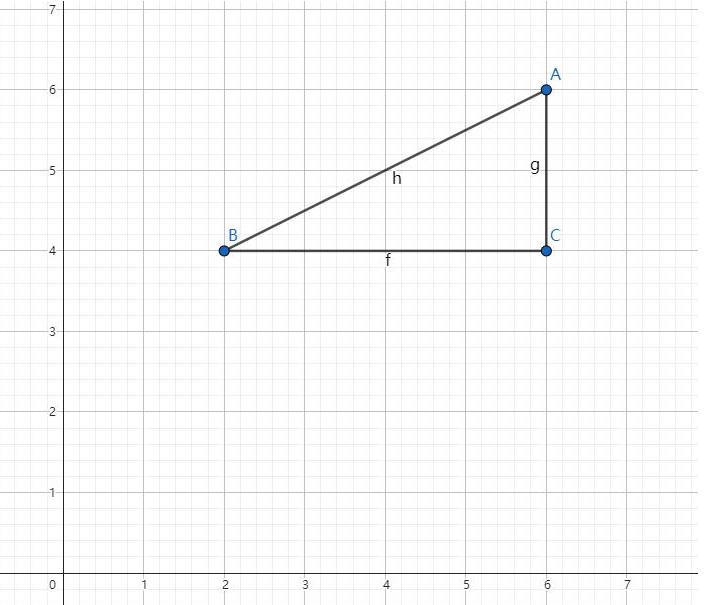
我們可以看到我們的 \(A,B\) 兩點，我們選了一箇中轉點 \(C\) 來幫助我們計算 \(|AB|\)，而選擇的 \(C\) 點與 \(A,B\) 構成了一個三角形，而我們要求的就是 \(h\)，但是很明顯是可以通過勾股定理來計算的，也就是 \(h=\sqrt{f^{2}+g^{2}}\)，而 \(f\) 的值就是 \(|x_{2}-x_{1}|\)，\(g\) 的值為 \(|y_{2}-y_{1}|\)，平方後絕對值可以不加，所以得到了上面的公式。

當然我們不一定只在平面上解決這個問題，有可能會遇到三維空間的問題，也就是立體空間裡面求解歐幾里得距離。

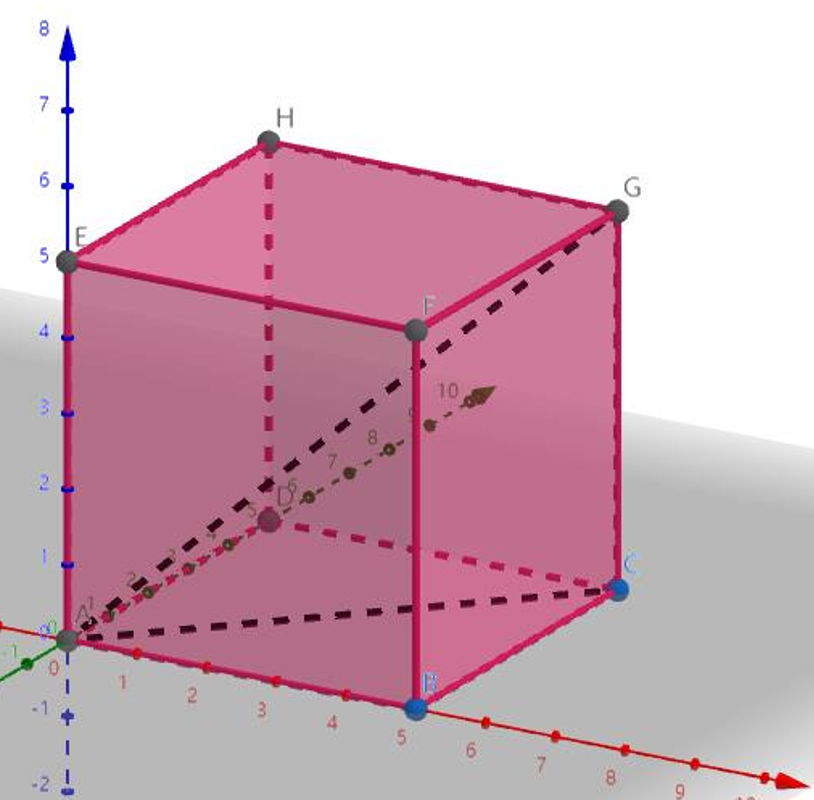
~~技術有限~~

我們可以看到我們要求的是 \(A(x1,y1,z1),G(x2,y2,z2)\) 兩點的距離 \(|AG|\)，我們考慮這樣來求解：

如果想要求 \(|AG|\)，我們從圖中可以看出 \(AG\) 是 \(A,G,C\) 所在平面的一個直角三角形的斜邊，而 \(GC\) 的長度我們是可以求出來的，就是 \(|z2-z1|\)，所以問題轉化為求 \(AC\) 的長度；\(AC\) 所在的平面為 \(ABCD\) ，我們可以直接用上面的公式來計算出 \(AC^{2}=(y2-y1)^{2}+(x2-y1)^{2}\)，然後跟 \(GC\) 勾股定理一下就可以得出以下公式：

\[|AG|=\sqrt{(x2-x1)^2+(y2-y1)^2+(z2-z1)^2} \]

由此我們也可以推廣到多維，但大多數情況用不到，~~而且我也不會證~~

雖然歐幾里得距離很有用，但也有缺點，比如最後得出的答案往往都是帶根號的，會存在一定的誤差，在資訊學裡這是一個難以解決的問題。

曼哈頓距離

在二維的空間內，兩個點之間的曼哈頓距離為他們橫座標之差的絕對值與縱座標之差的絕對值的和。設 \(A(x1,y1),B(x2,y2)\)，則兩點之間的曼哈頓距離可以表示為

\[d(A,B)=|x1-x2|+|y1-y2| \]

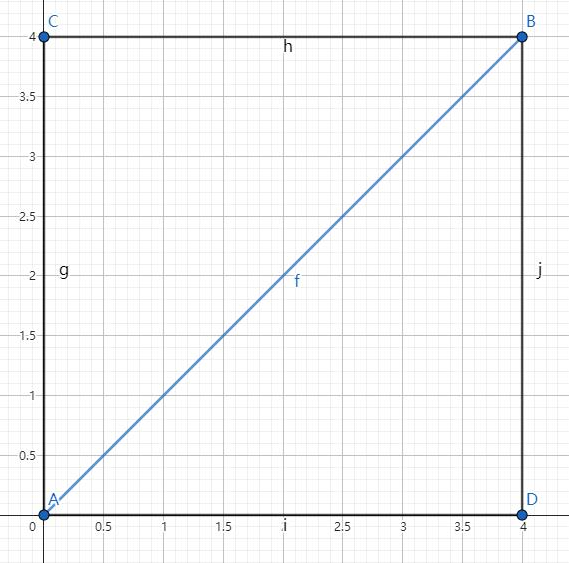
例如上圖中的藍線為歐幾里得距離，黑線為曼哈頓距離。

當然曼哈頓距離也可以通過類似歐幾里得距離的推理出 N 維空間的公式。

設 \(A(x1,x2,\dots,xn),B(y1,y2,\dots,yn)\)，則有：

\[d(A,B)=|x1-y1|+|x2-y2|+\dots+|xn-yn|\\ =\sum_{i=1}^{n}|xi-yi| \]

性質

曼哈頓距離有以下數學性質：

非負性，這一點很明顯就能看出來
統一性，點到自身的曼哈頓距離為 \(0\)。
對稱性，\(A\) 到 \(B\) 與 \(B\) 到 \(A\) 的曼哈頓距離相等。
三角不等式，從 \(i\) 到 \(j\) 的直接距離不會大於途經的任何其他點 \(k\) 的距離。\(d(i,j)\le d(i,k)+d(k,j)\)

切比雪夫距離

切比雪夫距離是向量空間中的一種度量，兩個點之間的距離定義為其各座標數值差的最大值。

在二維空間內，兩個點之間的切比雪夫距離為他們橫座標之差的絕對值和縱座標之差的絕對值的最大值。設 \(A(x1,y1),B(x2,y2)\)，則 \(A,B\) 之間的切比雪夫距離可以用公式表示為：

\[d(A,B)=\max(|x1-x2|,|y1-y2|) \]

\(n\) 維空間中 \(A(x1,x2,\dots,xn),B(y1,y2,\dots,yn)\) 的切比雪夫距離的公式可以表示為：

\[d(x,y)=\max\{|x1-y1|,|x2-y2|,\dots,|xn-yn|\} \]

曼哈頓距離與切比雪夫距離的相互轉化

首先我們考慮曼哈頓距離為 \(1\) 的所有點組成的影象：

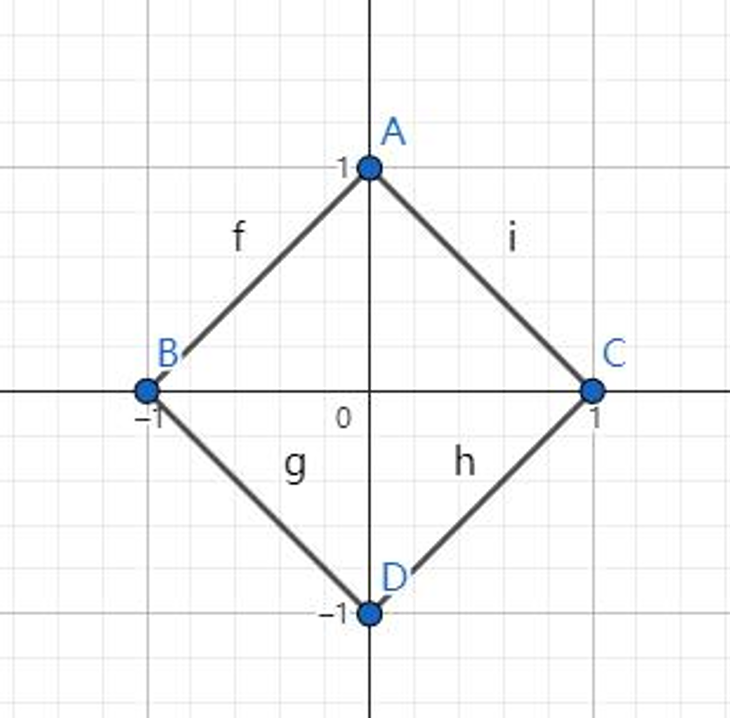
然後再來看看所有切比雪夫距離為 \(1\) 的影象：

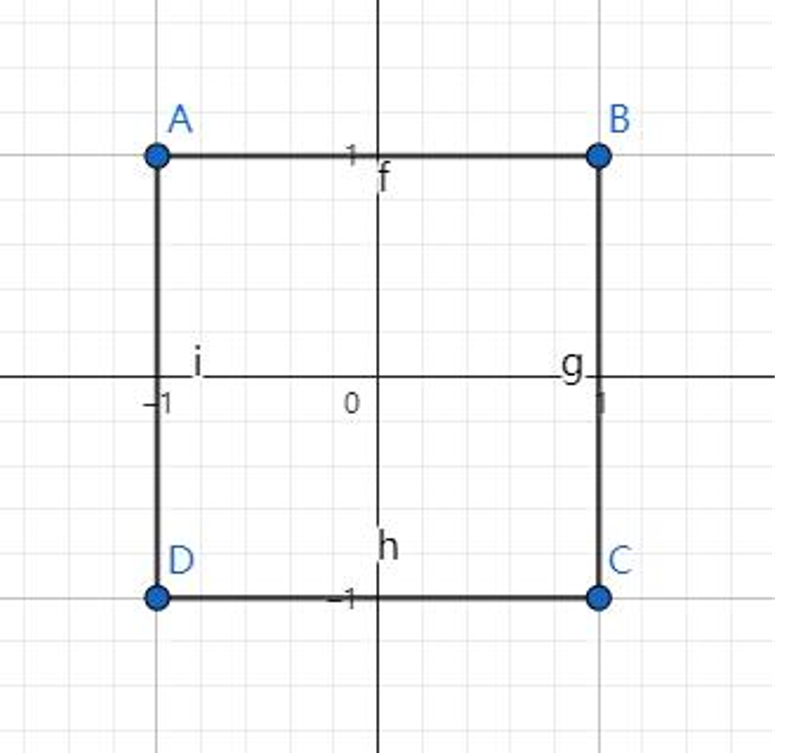
對比一下，你會發現，這兩個正方形是相似的。

所以我們可以找到曼哈頓距離與切比雪夫距離之間的關係！

我們假設 \(A(x1,y1),B(x2,y2)\)，我們把曼哈頓距離中的絕對值拆開，能夠得到四個值，這四個值中最大的是兩個非負數之和，即曼哈頓距離。則 \(A,B\) 兩點的曼哈頓距離為：

\[d(A,B)=|x1-x2|+|y1-y2|\\ =\max\{ x1-x2+y1-y2,x1-x2+y2-y1,x2-x1+y1-y2,x2-x1+y2-y1 \}\\ =\max(|(x1+y1)-(x2+y2)|,|(x1-y1)-(x2-y2)|) \]

欸，這不是 \((x1+y1,x1-y1)\) 與 \((x2+y2,x2-y2)\) 兩點的切比雪夫距離嗎？

所以，將點 \((x,y)\) 轉化為 \((x+y,x-y)\)，新座標系下的切比雪夫距離即為原座標系下的曼哈頓距離。

那我們是不是也可以用切比雪夫距離轉化成曼哈頓距離呢？

設 \(A(x1,y1),B(x2,y2)\) 的切比雪夫距離為：

\[d(A,B)=\max\{|x1-x2|,|y1-y2|\}\\ =\max\left\{ \left|\frac{x1+y1}{2}-\frac{x2+y2}{2}\right|+\left| \frac{x1-y1}{2}-\frac{x2-y2}{2} \right| \right\} \]

為什麼呢？

還記得上面的兩張圖嗎？把切比雪夫的轉 \(45^{\circ}\) 後再縮小至 \(\frac{1}{2}\) 不就是曼哈頓距離的了嗎？所以都帶有 \(\frac{1}{2}\) 這個係數。

也就是說，將每一個點 \((x,y)\) 轉化為 \((\frac{x+y}{2},\frac{x-y}{2})\)，新座標系下的曼哈頓距離即為原座標系下的切比雪夫距離。

結論

曼哈頓座標系是通過切比雪夫座標系旋轉 \(45^{\circ}\) 後，再縮小到原來的一半得到的。
將一個點 \((x,y)\) 的座標轉化為 \((x+y,x-y)\) 後，原座標系中的曼哈頓距離等於新座標系中的切比雪夫距離。
將一個點 \((x,y)\) 的座標轉化為 \((\frac{x+y}{2},\frac{x-y}{2})\) 後，原座標系中的切比雪夫距離等於新座標系中的曼哈頓距離。

碰到求切比雪夫距離或者曼哈頓距離的題目的時候，我們往往可以相互轉化來求解。

\(L_{m}\) 距離

一般的，我們定義平面上兩點 \(A(x1,y1),B(x2,y2)\) 之間的 \(L_{m}\) 距離為

\[d(L_{m})=(|x1-x2|^{m}+|y1-y2|^{m})^{\frac{1}{m}} \]

容易發現 \(L_{2}\) 就是歐幾里得距離，\(L_{1}\) 就是曼哈頓距離。

漢明距離

漢明距離是兩個字串之間的距離，它表示兩個長度相同的字串對應位字元不同的數量

通常用於比較兩個串的差異。

部分參考自https://www.luogu.com.cn/blog/xuxing/Distance-Algorithm

題目中常見的幾種距離

距離