視覺化學習：利用向量判斷多邊形邊界

引言

繼續鞏固我的視覺化學習，向量運算是計算機圖學的基礎，本例依舊是向量的一種應用，利用向量判斷多邊形邊界，但是多邊形的邊界判斷稍微有點複雜，所以除了應用向量之外，還需要藉助三角剖分的相關工具。這個例子中視覺化的展示採用Canvas2D來實現。

問題

假設Canvas畫布上存在一個如下多邊形：

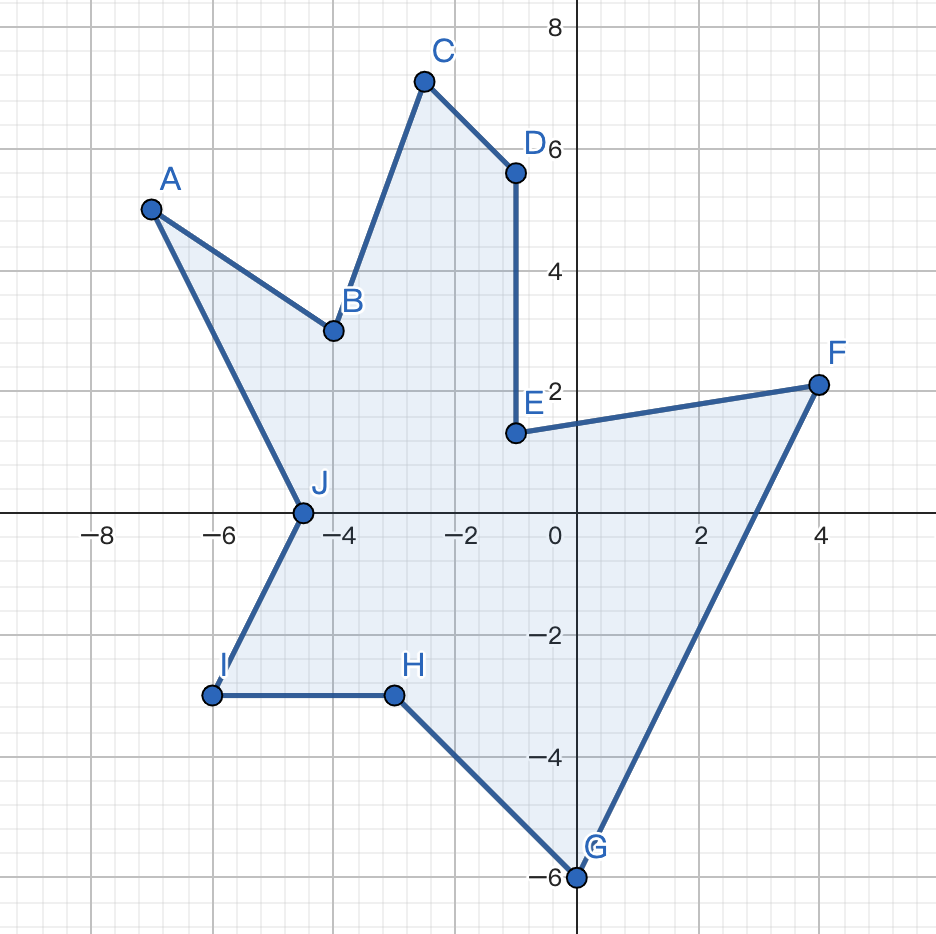
我們移動滑鼠的時候，想要實現一個效果，就是當滑鼠移動到多邊形內部的時候，將多邊形內部的填充顏色更新成其他顏色；所以此時我們需要判斷滑鼠是否在多邊形內部，這就涉及到多邊形邊界的判斷。

思路

首先我們先將這個多邊形繪製到Canvas畫布上。

<canvas width="512" height="512"></canvas>

canvas {
  width: 512px;
  height: 512px;
  border: 1px solid #eee;
}

const canvas = document.querySelector('canvas');
const ctx = canvas.getContext('2d');

ctx.translate(canvas.width / 2, canvas.height / 2);
ctx.scale(1, -1);

const vertices = [
    [ -179.2, 128 ],
    [ -102.4, 76.8 ],
    [ -64, 181.76 ],
    [ -25.6, 143.36 ],
    [ -25.6, 33.28 ],
    [ 102.4, 53.76 ],
    [ 0, -153.6 ],
    [ -76.8, -76.8 ],
    [ -153.6, -76.8 ],
    [ -115.2, 0 ]
];

drawPolygon(vertices);

function drawPolygon(vertices, fillStyle = "red") {
  ctx.beginPath();
  ctx.moveTo(...vertices[0]);
  for (let i = 1; i < vertices.length; i ++) {
      ctx.lineTo(...vertices[i]);
  }
  ctx.closePath();
  ctx.fillStyle = fillStyle;
  ctx.fill();
}

1. 呼叫API

對於Canvas2D而言，有一個API自帶的方法，就是CanvasRenderingContext2D的isPointInPath方法。

這個方法使用起來非常簡單，我們在這個時候直接增加一個滑鼠移動事件的監聽就可以。

const {left, top} = canvas.getBoundingClientRect();
canvas.addEventListener('mousemove', e => {
  const {x: pageX, y: pageY} = e;
  // 座標轉化
  const offsetX = x - left;
  const offsetY = y - top;
  // 清除畫布
  ctx.clearRect(-256, -256, 512, 512);
  if (ctx.isPointInPath(offsetX, offsetY)) {
    drawPolygon(vetices, "green");
  } else {
    drawPolygon(vetices);
  }
});

但是這個API的使用存在很大的侷限性，就是它只能針對當前繪製的圖形生效。

就比如說，如果在完成這個多邊形的繪製之後，又繪製了一個小三角形。

const triangle = [
  [100, 100], 
  [100, 200], 
  [150, 200]
];

drawPolygon(triangle, "blue");

為了保持這個小三角形，我們還需要修改滑鼠監聽事件，以達到更新畫布時，三角形依舊被繪製。

canvas.addEventListener('mousemove', e => {
  const {pageX: x, pageY: y} = e;
  // 座標轉化
  const offsetX = x - left;
  const offsetY = y - top;
  // 清除畫布
  ctx.clearRect(-256, -256, 512, 512);
  if (ctx.isPointInPath(offsetX, offsetY)) {
    drawPolygon(vertices, "green");
    drawPolygon(triangle, "blue");
  } else {
    drawPolygon(vertices);
    drawPolygon(triangle, "blue");
  }
});

此時我們再移動滑鼠，就會發現，在滑鼠移動到多邊形內部時，多邊形的填充顏色並不會變，但是當滑鼠移動到小三角形內部時，多邊形的填充色發生了變化；這就是Canvas2D Context的isPointInPath方法所存在的侷限性。

2. 自定義isPointInPath

為了突破Canvas2D API中自帶方法的侷限性，最簡單的方法就是，我們手動自定義一個自己的isPointInPath方法。

具體實現如下：

function isPointInPath(x, y) {
  // 根據ctx重新clone一個新的Canvas物件
  const cloned =  ctx.canvas.cloneNode().getContext('2d');
  cloned.translate(canvas.width / 2, canvas.height / 2);
  cloned.scale(1, -1);
  let ret = false;
  // 繪製多邊形，判斷點是否在圖形內部
  drawPolygon(cloned, vertices, "red");
  ret |= cloned.isPointInPath(x, y);
  if (!ret) {
    // 如果不在，繼續繪製小三角形，判斷點是否在圖形內部
    drawPolygon(cloned, triangle, "blue");
    ret |= cloned.isPointInPath(x, y);
  }
  return ret;
}

• 首先，根據原畫布的Context建立一個新的Canvas物件並獲取它的上下文
• 然後繪製多邊形，並判斷滑鼠是否在多邊形內部
• 如果不在多邊形內部，繼續判斷是否在三角形內部
• 最後將結果返回

可以看到，在這個自定義的方法內部，我們依然是呼叫了Canvas2D Context的isPointInPath方法。

接著我們還需要修改滑鼠的監聽事件，把判斷方法改為我們自定義的isPointInPath。

此時移動滑鼠，可以看到，當滑鼠移動到多邊形或者三角形內部，都可以使多邊形的填充色發生變化；這就是因為我們在自定義的isPointInPath中做的兩次判斷。

但是我們也能發現，雖然這種方式解決了我們在第一種方式中所碰到的問題，卻也存在其他問題，第一，是增加了很多無謂的Canvas繪圖操作；第二，是通用性差，如果圖形有修改，那麼isPointInPath方法就要跟著修改，並且這個方法依賴於Canvas2D的API，如果哪天修改了繪圖方式，比如改為使用WebGL，就不能使用了。

3. 通用型isPointInPath

所以我們需要實現一個更具通用性的isPointInPath方法：直接通過點與幾何圖形的數學關係來判斷點是否在圖形內，也就是我們標題中所說的利用向量來判斷。

但是直接判斷點與幾何圖形的關係，還是比較困難的。這個時候，我們可以先對多邊形進行三角剖分，三角剖分可以簡單地理解為是把多邊形表示成由多個三角形組合而成的形式；接著將點和對應的多個三角形的關係進行逐一判斷；最後得出結果。

對於三角剖分，涉及的演演算法稍複雜，這裡我們直接使用一個成熟的、使用起來比較簡單的庫——earcut；然後就剩下最關鍵的一步，就是點和三角形的位置判斷。

判斷點是否在三角形內部，就相對比較簡單了：

假設三角形的三個點是A、B、C，把三角形的三條邊分別使用向量表示，再將平面上一個點D連線三角形三個頂點得到三個向量，那麼點D在三角形內部的充分必要條件就是：

AB x AD、BC x BD、CA x CD三組向量的叉乘結果符號相同。就如下圖所示。

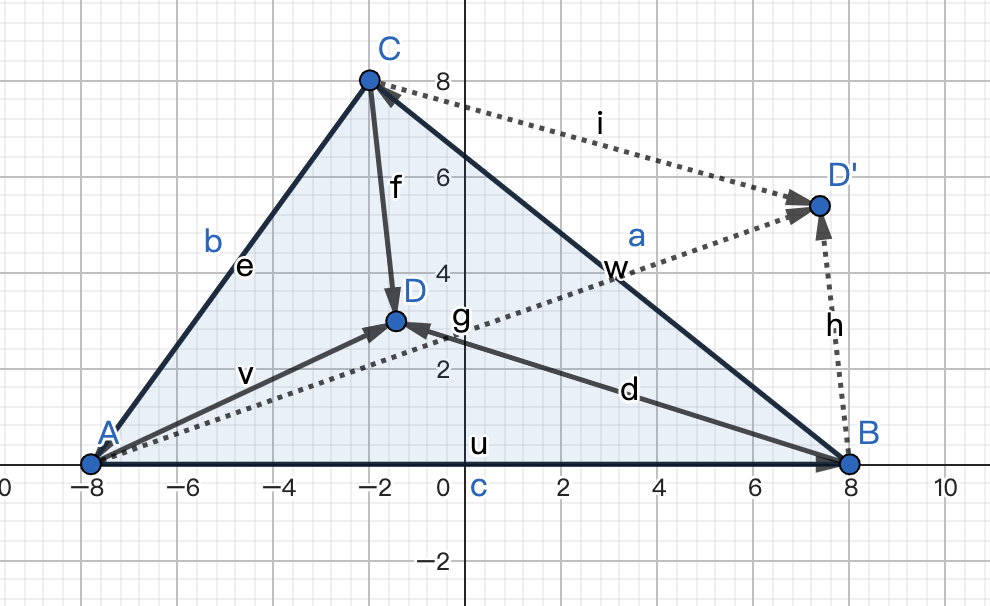
• 如果點在三角形內部，就如圖上的點D，可以看出AB 到 AD、BC 到 BD、CA 到 CD的旋轉方向都是逆時針，旋轉方向相同，所以最後的叉乘結果符號都是相同的；
• 而如果點在三角形外部，就如圖上的點D'，可以看出AB到AD'和CA到CD'的旋轉方向是逆時針，但BC到BD'的旋轉方向是順時針，所以三組向量叉乘的結果符號並不相同

因此根據上述條件，就可以定義一個簡單的判定函數：

function inTriangle(p1, p2, p3, point) {
    const a = p2.copy().minus(p1);
    const b = p3.copy().minus(p2);
    const c = p1.copy().minus(p3);

    const u1 = point.copy().minus(p1);
    const u2 = point.copy().minus(p2);
    const u3 = point.copy().minus(p3);

    const s1 = Math.sign(a.cross(u1));
    const s2 = Math.sign(b.cross(u2));
    const s3 = Math.sign(c.cross(u3));

    return s1 === s2 && s2 === s3;
}

這個函數的前三個引數是三角形的三個頂點，最後一個引數是待判斷的點；這樣就能判斷點是否在三角形內部了。

但是這個函數中還缺少一種特殊情況的判斷，就是點恰好在三角形某條邊上的情況。

如果一個點在三角形的一條邊上，那它需要滿足以下2個條件：

• 第一，它和所在邊某個頂點形成的向量與這個頂點所在邊的向量，這兩個向量的叉乘結果為0，即這兩個向量的夾角為180度或0度。比如點D在邊AB上，則AB x AD為0

• 第二，它和這個頂點形成的向量與這個頂點所在邊的向量，這兩個向量的點乘結果除以邊長的平方，結果大於等於0且小於等於1。比如點D在邊AB上，則0<= AB·AD/AB² <=1

  這個值也就是AD在AB上的投影的長度，與AB長度的比值，大於零，說明兩個向量的夾角是0度，為同一方向，小於等於1，也就說明點D線上段AB上。

根據這兩個條件，我們可以對上面的判定函數進行優化：

function inTriangle(p1, p2, p3, point) {
    const a = p2.copy().minus(p1);
    const b = p3.copy().minus(p2);
    const c = p1.copy().minus(p3);

    const u1 = point.copy().minus(p1);
    const u2 = point.copy().minus(p2);
    const u3 = point.copy().minus(p3);

    const s1 = Math.sign(a.cross(u1));
    let p = a.dot(u1) / a.length ** 2;
    if (s1 === 0 && p >= 0 && p <= 1) return true;
    const s2 = Math.sign(b.cross(u2));
    p = b.dot(u2) / b.length ** 2;
    if (s2 === 0 && p >= 0 && p <= 1) return true;
    const s3 = Math.sign(c.cross(u3));
    p = c.dot(u3) / c.length ** 2;
    if(s3 === 0 && p >= 0 && p <= 1) return true;

    return s1 === s2 && s2 === s3;
}

這樣我們就可以使用inTriangle函數對某個點是否在三角形內部進行判斷了。

現在我們來繼續完成對點在多邊形內部的判斷：

1. 首先使用earcut庫對多邊形進行三角剖分處理

   1. 引入earcut庫

      <script src="https://unpkg.com/[email protected]/dist/earcut.dev.js"></script>
      

   2. 因為earcut庫只接受扁平化的頂點資料，我們需要先用陣列的flat方法將頂點扁平化

      const points = vertices.flat();
      

   3. 然後我們就可以把扁平化後的資料傳給earcut進行處理了

      const triangles = earcut(points);
      console.log(triangles);
      

      根據列印結果，可以看到earcut的處理結果是一個陣列，這個triangles陣列的元素是頂點資料在vertices陣列中的下標；在這個陣列中，每三個元素所對應的頂點就構成一個三角形。

   這樣我們就完成了多邊形的三角剖分。

2. 接著逐個判斷點是否在每個三角形內部。

   // 判斷點是否在多邊形內部
   // 將多邊形進行三角剖分，然後判斷點是否在其中某個三角形內部
   function isPointInPolygon({vertices, cells}, point) {
       let ret = false;
       for(let i = 0; i < cells.length; i += 3) {
           const p1 = new Vector2D(...vertices[cells[i]]);
           const p2 = new Vector2D(...vertices[cells[i + 1]]);
           const p3 = new Vector2D(...vertices[cells[i + 2]]);
           if (inTriangle(p1, p2, p3, point)) {
               ret = true;
               break;
           }
       }
       return ret;
   }
   

   根據返回的布林值就可以知道點是否在多邊形內部。

3. 最後就是修改滑鼠監聽事件的處理程式。

   const {left, top} = canvas.getBoundingClientRect();
   canvas.addEventListener('mousemove', e => {
     const {pageX: x, pageY: y} = e;
     // 座標轉化
     const offsetX = x - left;
     const offsetY = y - top;
     ctx.clearRect(-256, -256, 512, 512);
   
     const point = new Vector2D((offsetX - canvas.width / 2), (canvas.height / 2 - offsetY)); // 因為Canvas經過座標轉換，所以這裡需要把頁面上點的座標也轉換一遍，才能正常判斷
     if (isPointInPolygon({
           vertices,
           cells: triangles
         }, point)
     ) {
       drawPolygon(vertices, "green");
       drawPolygon(triangle, "blue");
     } else {
       drawPolygon(vertices);
       drawPolygon(triangle, "blue");
     }
   });
   

   這裡需要注意，Canvas2D自帶的API在進行判斷時，應該是自動對滑鼠對應的點的座標進行了轉換，所以我們使用自定義的方法時，不能直接使用offsetX和offsetY，需要自己去將點的座標根據座標系的轉換計算出對應在畫布上的座標。

此時，我們再去移動滑鼠，就可以看到，當滑鼠移動到多邊形內部或者多邊形的邊時，多邊形的填充色發生了改變，也就說明我們的判斷生效了；這就成功應用了向量來判斷多邊形邊界。